题目内容
12.a,b,c是非直角△ABC中角A、B、C的对边,且sin2A+sin2B-sin2C=absinAsinBsin2C,则△ABC的面积为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
分析 由正弦定理化简已知等式可得a2+b2-c2=2a2b2sinCcosC,由余弦定理可求2abcosC=$\frac{1}{2}$absinC•4abcosC,结合cosC≠0,利用三角形面积公式即可化简求值得解.
解答 解:∵sin2A+sin2B-sin2C=absinAsinBsin2C,
∴由正弦定理可得:a2+b2-c2=2a2b2sinCcosC,
∴2abcosC=$\frac{1}{2}$absinC•4abcosC,
∵cosC≠0,
∴S△ABC=$\frac{1}{2}$absinC=$\frac{2abcosC}{4abcosC}$=$\frac{1}{2}$.
故选:A.
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
2.已知集合M={x|4-x2>0},N={x|1≤2x<13,x∈Z},则M∩N=( )
| A. | {0} | B. | {0,1} | C. | {0,1,2} | D. | {0,1,2,3} |
1.某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
(Ⅰ)写出价格f(x)关于时间x的函数关系式(x表示投放市场的第x天,x∈N*);
(Ⅱ)销售量g(x)与时间x的函数关系式为$g(x)=-\frac{1}{3}x+\frac{109}{3}({1≤x≤100,x∈{N^*}})$,则该产品投放市场第几天的销售额最高?最高为多少千元?
| 时间 | 第4天 | 第32天 | 第60天 | 第90天 |
| 价格(千元) | 23 | 30 | 22 | 7 |
(Ⅱ)销售量g(x)与时间x的函数关系式为$g(x)=-\frac{1}{3}x+\frac{109}{3}({1≤x≤100,x∈{N^*}})$,则该产品投放市场第几天的销售额最高?最高为多少千元?
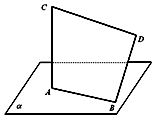 如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.
如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.