题目内容

7．已知函数f（x）=lnx+2x-6的零点位于区间（m-1，m）（m∈Z）内，则${27}^{\frac{1}{m}}$+log3m=（　　）
A．1B．2C．3D．4

分析 分别求出f（2）和f（3）并判断符号，再由函数的单调性判断出函数唯一零点所在的区间，即可求出m，从而可求${27}^{\frac{1}{m}}$+log3m．

解答 解：∵f（2）=ln2-2＜0，f（3）=ln3＞0，
∴f（x）=lnx+2x-6的存在零点x0∈（2，3）．
∵f（x）=lnx+2x-6在定义域（0，+∞）上单调递增，
∴f（x）=lnx+2x-6的存在唯一的零点x0∈（2，3）．
则整数m=3．
∴${27}^{\frac{1}{m}}$+log3m=3+1=4
故选D．

点评 本题主要考查函数零点存在性的判断方法的应用，要判断个数需要判断函数的单调性，属于基础题．

练习册系列答案
相关题目
17．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＜0}）$的右焦点且垂于x轴的直线与双曲线交于A，B两点，与双曲线的渐近线交于C，D两点，若|AB|≥$\frac{5}{13}|{CD}$|，则双曲线离心率的取值范围为$[{\frac{13}{12}，+∞}）$．
18．点O是平面上一定点，A、B、C是平面上△ABC的三个顶点，∠B、∠C分别是边AC、AB的对角，以下命题正确的是①②③④⑤（把你认为正确的序号全部写上）．
①动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$，则△ABC的重心一定在满足条件的P点集合中；
②动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ（$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$）（λ＞0），则△ABC的内心一定在满足条件的P点集合中；
③动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ（$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|sinB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|sinC}$）（λ＞0），则△ABC的重心一定在满足条件的P点集合中；
④动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ（$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}$）（λ＞0），则△ABC的垂心一定在满足条件的P点集合中；
⑤动点P满足$\overrightarrow{OP}$=$\frac{\overrightarrow{OB}+\overrightarrow{OC}}{2}$+λ（$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}$）（λ＞0），则△ABC的外心一定在满足条件的P点集合中．
15．已知函数f（x）=alnx-x+$\frac{1}{x}$，g（x）=x2+x-b，y=f（x）的图象恒过定点P，且P点既在y=g（x）的图象上，又在y=f（x）的导函数的图象上．
（1）求a，b的值；
（2）设h（x）=$\frac{f（x）}{g（x）}$，当x＞0且x≠1时，判断h（x）的符号，并说明理由；
（3）求证：1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$＞lnn+$\frac{n+1}{2n}$（n≥2且n∈N*）．
2．如图所示是一个组合几何体的三视图，则该几何体的体积为（　　）
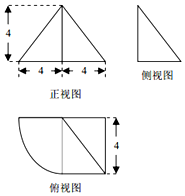
A．$\frac{16}{3}$πB．$\frac{64}{3}$C．$\frac{16π+64}{3}$D．16π+64
12．a，b，c是非直角△ABC中角A、B、C的对边，且sin2A+sin2B-sin2C=absinAsinBsin2C，则△ABC的面积为（　　）
A．$\frac{1}{2}$B．1C．2D．4
19．已知函数f（x）=sinx（x≥-3π），将f（x）的零点从小到大排列，得到一个数列{an}（n∈N*）
（1）直接写出{an}的通项公式；
（2）求{|an|}的前n项和Sn；
（3）设bn=$\frac{{a}_{n}}{π}$+4，证明：$\frac{1}{{b}_{1}}$+$\frac{1}{{{b}_{1}b}_{2}}$+$\frac{1}{{{{b}_{1}b}_{2}b}_{3}}$+$\frac{1}{{{{{b}_{1}b}_{2}b}_{3}b}_{4}}$+…+$\frac{1}{{{{b}_{1}b}_{2}b}_{3}••{•b}_{2017}}$＜2．
16．已知函数f（x）=x2-2（a-1）x+2在区间（-∞，5]上为减函数，则实数a的取值范围为[6，+∞）．
17．若复数z=3-2i，则z的共轭复数$\overline{z}$（　　）
A．-3+2iB．-3-2iC．-2+3iD．3+2i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网