题目内容
已知△ABC中,A(1,3),AB、AC边上的中线所在直线方程分别为x-2y+1=0和y-1=0,则边BC所在直线方程为 .
考点:直线的一般式方程
专题:直线与圆
分析:由题意设B(xB,1),则AB的中点D(
,2),由D在中线CD可得
-2×2+1=0,解方程可得B(5,1),同理可得C(-3,-1),易得直线的方程.
| xB+1 |
| 2 |
| xB+1 |
| 2 |
解答:
解:由题意设B(xB,1),则AB的中点D(
,2)
∵D在中线CD:x-2y+1=0上,∴
-2×2+1=0,
解得xB=5,即B(5,1).
同理∵点C在直线x-2y+1=0上,可以设C为(2yC-1,yC),
由
=1可解得yC=-1,即C(-3,-1).
∴直线BC的方程为y-1=
(x-5),
化为一般式可得x-4y-1=0,
故答案为:x-4y-1=0
| xB+1 |
| 2 |
∵D在中线CD:x-2y+1=0上,∴
| xB+1 |
| 2 |
解得xB=5,即B(5,1).
同理∵点C在直线x-2y+1=0上,可以设C为(2yC-1,yC),
由
| yC+3 |
| 2 |
∴直线BC的方程为y-1=
| -1-1 |
| -3-5 |
化为一般式可得x-4y-1=0,
故答案为:x-4y-1=0
点评:本题考查直线的一般式方程,求出B和C的坐标是解决问题的关键,属基础题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
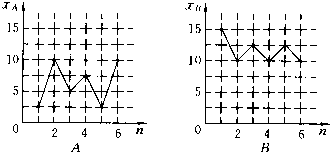
如图:样本A和B分别取自两个不同的总体,他们的样本平均数分别为
A和
B,样本标准差分别为sA和sB,则( )
. |
| x |
. |
| x |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在分别标有号码2,3,4,…,10的9张卡片中,随机取出两张卡片,记下它们的标号,则较大标号被较小标号整除的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若变量x,y满足约束条件
,则z=2x+3y的最小值为( )
|
| A、17 | B、14 | C、5 | D、3 |