题目内容
5.求证不等式:-1<$\frac{1}{2}$+$\frac{2}{5}$+$\frac{3}{10}$+…+$\frac{n}{{n}^{2}+1}$-lnn≤$\frac{1}{2}$,n∈N*.分析 n=1时,$\frac{1}{2}$+$\frac{2}{5}$+$\frac{3}{10}$+…+$\frac{n}{{n}^{2}+1}$-lnn=$\frac{1}{2}$,结论成立;n≥2时,$\frac{1}{n+1}$<$\frac{n}{{n}^{2}+1}$<$\frac{1}{n}$,证明:-1<$\frac{1}{2}$+$\frac{2}{5}$+$\frac{3}{10}$+…+$\frac{n}{{n}^{2}+1}$-lnn<$\frac{1}{2}$,n∈N*.就是要证明:-1<$\frac{1}{3}$+…+$\frac{1}{n+1}$-lnn,且$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$-lnn<$\frac{1}{2}$,n≥2,n∈N*.分别构造函数,即可证明结论.
解答 证明:n=1时,$\frac{1}{2}$+$\frac{2}{5}$+$\frac{3}{10}$+…+$\frac{n}{{n}^{2}+1}$-lnn=$\frac{1}{2}$,满足:-1<$\frac{1}{2}$+$\frac{2}{5}$+$\frac{3}{10}$+…+$\frac{n}{{n}^{2}+1}$-lnn≤$\frac{1}{2}$,
n≥2时,$\frac{1}{n+1}$<$\frac{n}{{n}^{2}+1}$<$\frac{1}{n}$,证明:-1<$\frac{1}{2}$+$\frac{2}{5}$+$\frac{3}{10}$+…+$\frac{n}{{n}^{2}+1}$-lnn<$\frac{1}{2}$,n∈N*.
就是要证明:-1<$\frac{1}{3}$+…+$\frac{1}{n+1}$-lnn,且$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$-lnn<$\frac{1}{2}$,n≥2,n∈N*.
令f(x)=$\frac{1-x}{x}$+lnx,则f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{1}{x}$,
当x≥1时,f′(x)≥0,∴f(x)在[1,+∞)上为增函数,
∴n≥2时:f($\frac{n}{n-1}$)=ln$\frac{n}{n-1}$-$\frac{1}{n}$>f(1)=0,
即:$\frac{1}{n}$<ln$\frac{n}{n-1}$,
∴$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$<lnn,
∴$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$-lnn<$\frac{1}{2}$.
令g(x)=ln(x+1)-x,则g′(x)=$\frac{1}{x+1}$-1,
当x≥1时,g′(x)<0,∴g(x)在[1,+∞)上减函数,
∴n≥2时:g($\frac{1}{n}$)=ln$\frac{n+1}{n}$-$\frac{1}{n}$<g(1)<0,
即:$\frac{1}{n}$>ln$\frac{n+1}{n}$,
∴$\frac{1}{3}$+…+$\frac{1}{n+1}$>ln(n+1)-ln2>lnn-1
∴-1<$\frac{1}{3}$+…+$\frac{1}{n+1}$-lnn,
综上所述,-1<$\frac{1}{2}$+$\frac{2}{5}$+$\frac{3}{10}$+…+$\frac{n}{{n}^{2}+1}$-lnn≤$\frac{1}{2}$,n∈N*.
点评 本题考查了利用构造函数法证明数列不等式,考查导数知识的运用,是难题,正确构建函数是关键.

| A. | $3\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | 3 |
| A. | 12 | B. | 20 | C. | $2\sqrt{3}$ | D. | $2\sqrt{5}$ |
| A. | 3x+4y+15=0 | B. | x=-3或3x+4y+15=0 | ||
| C. | x=-3或y=-$\frac{3}{2}$ | D. | x=-3 |
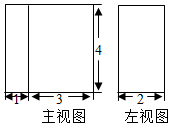
| A. | 20 | B. | 28 | C. | 20或32 | D. | 20或28 |
| A. | (1,$\frac{5}{4}$) | B. | ($\frac{5}{4}$,+∞) | C. | (1,+∞) | D. | (-∞,$\frac{5}{4}$) |