题目内容
6.为得到函数y=2cos2x-$\sqrt{3}$sin2x的图象,只需将函数y=2sin2x+1的图象( )| A. | 向左平移$\frac{π}{12}$个长度单位 | B. | 向右平移$\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{5π}{12}$个长度单位 | D. | 向右平移$\frac{5π}{12}$个长度单位 |
分析 利用三角函数的恒等变换化简函数的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:∵y=2cos2x-$\sqrt{3}$sin2x=cos2x-$\sqrt{3}$sin2x+1=2sin($\frac{π}{6}$-2x)+1
=-2sin(2x-$\frac{π}{6}$)+1=2sin(2x+$\frac{5π}{6}$)+1,
将函数y=2sin2x+1的图象向左平移$\frac{5π}{12}$个长度单位,可得得到函数y=2sin(2x+$\frac{5π}{6}$)+1的图象,
故选:C.
点评 本题主要考查三角函数的恒等变换,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
1.已知点M在角θ终边的延长线上,且|OM|=2,则M的坐标为( )
| A. | (2cosθ,2sinθ) | B. | (-2cosθ,2sinθ) | C. | (-2cosθ,-2sinθ) | D. | (2cosθ,-2sinθ) |
18.若tan(α+80°)=4sin420°,则tan(α+20°)的值为( )
| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{3\sqrt{3}}{5}$ | C. | $\frac{\sqrt{3}}{19}$ | D. | $\frac{\sqrt{3}}{7}$ |
 在直角梯形ABCD中,AB∥DC,AD⊥AB,AD=AB=2DC=2,点E、F分别在线段DC、AB上,设$\overrightarrow{DE}$=λ$\overrightarrow{DC}$,$\overrightarrow{AF}$=λ$\overrightarrow{AB}$,则$\overrightarrow{AE}$•$\overrightarrow{CF}$的最小值为-$\frac{33}{8}$.
在直角梯形ABCD中,AB∥DC,AD⊥AB,AD=AB=2DC=2,点E、F分别在线段DC、AB上,设$\overrightarrow{DE}$=λ$\overrightarrow{DC}$,$\overrightarrow{AF}$=λ$\overrightarrow{AB}$,则$\overrightarrow{AE}$•$\overrightarrow{CF}$的最小值为-$\frac{33}{8}$.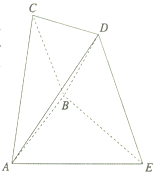 在如图所示的空间几何体中,边长为2的正三角形ABC所在平面与正三角形ABE所在平面互相垂直,DE在平面ABE内的射影为∠AEB的平分线且DE与平面AEB所成的角为60°,DE=2.
在如图所示的空间几何体中,边长为2的正三角形ABC所在平面与正三角形ABE所在平面互相垂直,DE在平面ABE内的射影为∠AEB的平分线且DE与平面AEB所成的角为60°,DE=2.