题目内容
17. 在直角梯形ABCD中,AB∥DC,AD⊥AB,AD=AB=2DC=2,点E、F分别在线段DC、AB上,设$\overrightarrow{DE}$=λ$\overrightarrow{DC}$,$\overrightarrow{AF}$=λ$\overrightarrow{AB}$,则$\overrightarrow{AE}$•$\overrightarrow{CF}$的最小值为-$\frac{33}{8}$.
在直角梯形ABCD中,AB∥DC,AD⊥AB,AD=AB=2DC=2,点E、F分别在线段DC、AB上,设$\overrightarrow{DE}$=λ$\overrightarrow{DC}$,$\overrightarrow{AF}$=λ$\overrightarrow{AB}$,则$\overrightarrow{AE}$•$\overrightarrow{CF}$的最小值为-$\frac{33}{8}$.
分析 用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{AE},\overrightarrow{CF}$,计算$\overrightarrow{AE}$•$\overrightarrow{CF}$得出关于λ的二次函数,利用二次函数的性质和λ的范围得出最小值.
解答 解:$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}$=$\overrightarrow{AD}+λ\overrightarrow{DC}$=$\overrightarrow{AD}+\frac{λ}{2}\overrightarrow{AB}$,
$\overrightarrow{CF}=\overrightarrow{CD}+\overrightarrow{DA}+\overrightarrow{AF}$=-$\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AD}$+$λ\overrightarrow{AB}$=($λ-\frac{1}{2}$)$\overrightarrow{AB}-\overrightarrow{AD}$,
∵AD⊥AB,AD=AB=2DC=2,
∴${\overrightarrow{AD}}^{2}$=${\overrightarrow{AB}}^{2}$=4,$\overrightarrow{AB}•\overrightarrow{AD}=0$,
∴$\overrightarrow{AE}•\overrightarrow{CF}$=($\overrightarrow{AD}+\frac{λ}{2}\overrightarrow{AB}$)•[($λ-\frac{1}{2}$)$\overrightarrow{AB}-\overrightarrow{AD}$]=$\frac{2{λ}^{2}-λ}{4}$${\overrightarrow{AB}}^{2}$-${\overrightarrow{AD}}^{2}$=2λ2-λ-4=2(λ-$\frac{1}{4}$)2-$\frac{33}{8}$,
∴当λ=$\frac{1}{4}$时,$\overrightarrow{AE}•\overrightarrow{CF}$取得最小值-$\frac{33}{8}$.
故答案为:-$\frac{33}{8}$.
点评 本题考查了平面向量的几何运算,数量积运算,属于中档题.

| A. | 向左平移$\frac{π}{12}$个长度单位 | B. | 向右平移$\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{5π}{12}$个长度单位 | D. | 向右平移$\frac{5π}{12}$个长度单位 |
 如图,在△ABC中,∠BAC=90°,AB=6,D在斜边BC上,且CD=3DB,则$\overrightarrow{AB}•\overrightarrow{CD}$=27.
如图,在△ABC中,∠BAC=90°,AB=6,D在斜边BC上,且CD=3DB,则$\overrightarrow{AB}•\overrightarrow{CD}$=27. 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,AB=BC=$\frac{1}{2}$CD,E为AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,AB=BC=$\frac{1}{2}$CD,E为AA1的中点.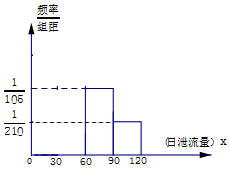 某地政府在该地一水库上建造一座水电站,用泄流水量发电,如图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120],历年中日泄流量在区间[30,60)的年平均天数为156天,一年按364天计.
某地政府在该地一水库上建造一座水电站,用泄流水量发电,如图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120],历年中日泄流量在区间[30,60)的年平均天数为156天,一年按364天计.