题目内容
11.函数y=3-2sinx的单调递增区间为[$\frac{π}{2}$+2kπ,$\frac{3π}{2}$+2kπ](k∈z).分析 根据正弦函数的单调性写出函数y=3-2sinx的单调递增区间.
解答 解:正弦函数y=sinx的单调减区间是:
[$\frac{π}{2}$+2kπ,$\frac{3π}{2}$+2kπ],k∈Z;
∴函数y=3-2sinx的单调递增区间是:
[$\frac{π}{2}$+2kπ,$\frac{3π}{2}$+2kπ],k∈Z.
故答案为:[$\frac{π}{2}$+2kπ,$\frac{3π}{2}$+2kπ],k∈Z.
点评 本题考查了正弦函数的单调性与单调区间的应用问题,是基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
1.已知条件p:函数$y=\sqrt{\frac{x-1}{x+3}}$的定义域,条件q:5x-6>x2,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
19.过双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的右焦点F作双曲线的一条渐近线的垂线,垂足为E,O为坐标原点,若∠OFE=2∠EOF,则b=( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{\sqrt{3}}{3}$ |
6.为得到函数y=2cos2x-$\sqrt{3}$sin2x的图象,只需将函数y=2sin2x+1的图象( )
| A. | 向左平移$\frac{π}{12}$个长度单位 | B. | 向右平移$\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{5π}{12}$个长度单位 | D. | 向右平移$\frac{5π}{12}$个长度单位 |
16.已知圆C:x2+y2=1,直线l:y=k(x+2),在[-1,1]上随机选取一个数k,则事件“直线l与圆C相离
”发生的概率为( )
”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2-\sqrt{2}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{2-\sqrt{3}}{2}$ |
3.若tanα=4sin420°,则tan(α-60°)的值为( )
| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{3\sqrt{3}}{5}$ | C. | $\frac{\sqrt{3}}{7}$ | D. | $\frac{\sqrt{3}}{19}$ |
20.某几何体的三视图如图所示,则该几何体的表面积为( )
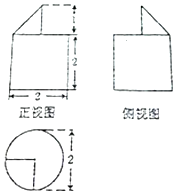

| A. | 6π+1 | B. | $\frac{{({24+\sqrt{2}})π}}{4}+1$ | C. | $\frac{{({23+\sqrt{2}})π}}{4}+\frac{1}{2}$ | D. | $\frac{{({23+\sqrt{2}})π}}{4}+1$ |
 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,AB=BC=$\frac{1}{2}$CD,E为AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,AB=BC=$\frac{1}{2}$CD,E为AA1的中点.