题目内容
16.若f(x)+3f(-x)=log2(x+3),则f(1)=$\frac{1}{8}$.分析 由已知条件联立方程组求出f(x)=$\frac{1}{8}$[3log2(3-x)-log2(x+3)],由此能求出f(1).
解答 解:∵f(x)+3f(-x)=log2(x+3),①
∴f(-x)+3f(x)=log2(3-x),②
②×3-①,得:8f(x)=3log2(3-x)-log3(x+3),
∴f(x)=$\frac{1}{8}$[3log2(3-x)-log2(x+3)],
∴f(1)=$\frac{1}{8}$(3log22-log24)=$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
6.为得到函数y=2cos2x-$\sqrt{3}$sin2x的图象,只需将函数y=2sin2x+1的图象( )
| A. | 向左平移$\frac{π}{12}$个长度单位 | B. | 向右平移$\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{5π}{12}$个长度单位 | D. | 向右平移$\frac{5π}{12}$个长度单位 |
4.已知集合M={x|x2-3x=0},N={x|x>-1},则M∩N=( )
| A. | (-1,0) | B. | (0,3) | C. | {0,3} | D. | {3} |
11.某四棱锥的三视图如图所示,该四棱锥的侧面积为( )


| A. | 8 | B. | 16$\sqrt{2}$ | C. | 10 | D. | 6$\sqrt{2}$ |
5.已知A=[1,+∞),$B=\left\{{x∈R|\frac{1}{2}≤x≤2a-1}\right\}$,若A∩B≠∅,则实数a的取值范围是( )
| A. | [1,+∞) | B. | $[{\frac{1}{2},1}]$ | C. | $[{\frac{2}{3},+∞})$ | D. | (1,+∞) |
6.已知函数f(x)=-x5-x3-5x+2,若f(a2)+f(a-2)>4,则实数a的取值范围( )
| A. | (-∞,1) | B. | (-∞,3) | C. | (-2,1) | D. | (-1,2) |
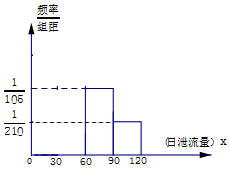 某地政府在该地一水库上建造一座水电站,用泄流水量发电,如图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120],历年中日泄流量在区间[30,60)的年平均天数为156天,一年按364天计.
某地政府在该地一水库上建造一座水电站,用泄流水量发电,如图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120],历年中日泄流量在区间[30,60)的年平均天数为156天,一年按364天计.