题目内容
9．若lgx+lgy=2，求5x+2y的最小值．分析 由lgx+lgy=2得x＞0，y＞0，xy=100；从而利用基本不等式求解．
解答 解：∵lgx+lgy=2，
∴x＞0，y＞0，xy=100；
∴5x+2y≥2$\sqrt{5x•2y}$=2$\sqrt{1000}$=20$\sqrt{10}$．
（当且仅当5x=2y，即x=2$\sqrt{10}$，y=5$\sqrt{10}$时，等号成立）．
点评 本题考查了对数运算的性质及基本不等式的化简与运算．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
17．两条直线l1：x-3y+1=0与直线l2：x+2y-5=0的夹角是（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{π}{4}$ | C． | $\frac{3π}{4}$ | D． | arctan$\sqrt{2}$ |
4．
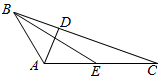如图所示，在三角形ABC中，AD⊥BC，AD=1，BC=4，点E为AC的中点，$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$，则AB的长度为（ ）
如图所示，在三角形ABC中，AD⊥BC，AD=1，BC=4，点E为AC的中点，$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$，则AB的长度为（ ）| A． | 2 | B． | $\frac{3}{2}$ | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |