题目内容
10.如果复数z满足|z|=1且z2=a+bi,其中a,b∈R,则a+b的最大值是$\sqrt{2}$.分析 由|z|=1,得|z2|=1,结合z2=a+bi,得a2+b2=1,然后利用基本不等式求得a+b的最大值.
解答 解:∵|z|=1,∴|z2|=1,
由z2=a+bi,得a2+b2=1,
∴(a+b)2≤2(a2+b2)=2,
故当$a=b=\frac{\sqrt{2}}{2}$时,a+b的最大值是$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查复数模的求法,训练了利用基本不等式求最值,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列函数中,在其定义域内既是奇函数又是单调递增的函数是( )
| A. | y=-$\frac{1}{x}$ | B. | y=3-x-3x | C. | y=x|x| | D. | y=x3-x |
5.线段AD、BE分别时边长为2的等边三角形ABC在边BC、AC边上的高,则$\overrightarrow{AD}$•$\overrightarrow{BE}$=( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
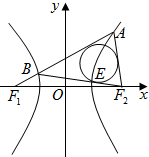 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,|F1F2|=4,点A在双曲线的右支上,线段AF1与双曲线左支相交于点B,△F2AB的内切圆与边BF2相切于点E.若|AF2|=2|BF1|,|BE|=2$\sqrt{2}$,则双曲线C的离心率为$\sqrt{2}$.
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,|F1F2|=4,点A在双曲线的右支上,线段AF1与双曲线左支相交于点B,△F2AB的内切圆与边BF2相切于点E.若|AF2|=2|BF1|,|BE|=2$\sqrt{2}$,则双曲线C的离心率为$\sqrt{2}$.