题目内容
已知函数f(x)的导函数为f′(x),且满足f(x)=3x2+2xf′(2),则f′(3)= .
考点:导数的运算
专题:导数的概念及应用
分析:求函数的导数,先求出f′(2),即可.
解答:
解:∵f(x)=3x2+2xf′(2),
∴f′(x)=6x+2f′(2),
则f′(2)=6×2+2f′(2),
解得f′(2)=-12,
则f′(x)=6x-24,
∴f′(3)=18-24=-6,
故答案为:-6
∴f′(x)=6x+2f′(2),
则f′(2)=6×2+2f′(2),
解得f′(2)=-12,
则f′(x)=6x-24,
∴f′(3)=18-24=-6,
故答案为:-6
点评:本题主要考查函数的导数的计算,要求熟练掌握常见函数的导数公式,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知定义在R上的函数满足f(1)=5,且f(x)的导函数f′(x)<2x+3,则不等式f(x)<x2+3x+1的解集为( )
| A、{x|-1<x<1} |
| B、{x|x<1} |
| C、{x|x>1} |
| D、{x|x<-1或x>1} |
计算cos300°的值( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
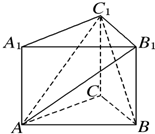 如图所示,已知三棱柱ABC A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则
如图所示,已知三棱柱ABC A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则 设f(x)是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图象,则f(2014)+f(2015)=( )
设f(x)是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图象,则f(2014)+f(2015)=( )