题目内容
 设f(x)是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图象,则f(2014)+f(2015)=( )
设f(x)是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图象,则f(2014)+f(2015)=( )| A、3 | B、2 | C、1 | D、0 |
考点:函数的周期性
专题:函数的性质及应用
分析:根据函数的周期性以及函数的图象进行求解即可.
解答:
解:由图象知f(1)=1,f(-1)=2,
∵f(x)是定义在R上的周期为3的周期函数,
∴f(2014)+f(2015)=f(1)+f(-1)=1+2=3,
故选:A
∵f(x)是定义在R上的周期为3的周期函数,
∴f(2014)+f(2015)=f(1)+f(-1)=1+2=3,
故选:A
点评:本题主要考查函数值的求解,根据函数的周期性进行转化是解决本题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
点M(1,1),点N(4,5),则|MN|=( )
| A、1 | B、2 | C、3 | D、5 |
若f(x)是定义在[-2,2]上的奇函数,且在[0,2]上单调递减,若f(m)+f(m-1)<0,则实数m的取值范围是( )
A、[-1,
| ||
B、(
| ||
C、(
| ||
D、(-∞,
|
要得到函数y=2cos(2x-
)的图象,只要将函数y=2cos2x的图象( )
| π |
| 6 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
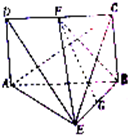 如图,已知四棱锥E-ABCD的底面ABCD是平行四边形,AE⊥BE,平面ACE⊥平面BCE,
如图,已知四棱锥E-ABCD的底面ABCD是平行四边形,AE⊥BE,平面ACE⊥平面BCE,