题目内容
15.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-6≤0}\\{x-y-1≤0}\\{x-1≥0}\end{array}\right.$,若z=ax+2y仅在点($\frac{7}{3}$,$\frac{4}{3}$)处取得最大值,则a的值可以为( )| A. | -8 | B. | -4 | C. | 4 | D. | 8 |
分析 画出约束条件的可行域,求出顶点坐标,利用z=ax+2y仅在点($\frac{7}{3}$,$\frac{4}{3}$)处取得最大值,利用斜率关系求解即可.
解答  解:如图所示,约束条件$\left\{\begin{array}{l}{2x+y-6≤0}\\{x-y-1≤0}\\{x-1≥0}\end{array}\right.$所表示的区域为图中阴影部分:其中A(1,0),B($\frac{7}{3}$,$\frac{4}{3}$),C(1,4),
解:如图所示,约束条件$\left\{\begin{array}{l}{2x+y-6≤0}\\{x-y-1≤0}\\{x-1≥0}\end{array}\right.$所表示的区域为图中阴影部分:其中A(1,0),B($\frac{7}{3}$,$\frac{4}{3}$),C(1,4),
依题意z=ax+2y仅在点($\frac{7}{3}$,$\frac{4}{3}$)处取得最大值,可得$-\frac{a}{2}<-2$,即,a>4.
故选:D.
点评 本题考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
5.已知平面直角坐标系内的两个向量$\overrightarrow a=(m,3m-4)$,$\overrightarrow b=(1,2)$,且平面内的任一向量$\overrightarrow{c}$都可以唯一的表示成$\overrightarrow{c}$=$λ\overrightarrow{a}$+$μ\overrightarrow{b}$(λ,μ为实数),则m的取值范围是( )
| A. | (-∞,4) | B. | (4,+∞) | C. | (-∞,4)∪(4,+∞) | D. | (-∞,+∞) |
6.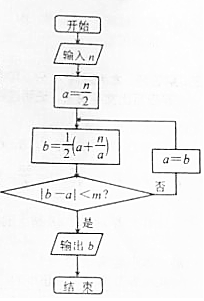 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )| A. | 0.6 | B. | 0.1 | C. | 0.01 | D. | 0.05 |
10.已知集合M={x|x2≤1},N={x|log2x<1},则M∩N=( )
| A. | [-1,2) | B. | [-1,1] | C. | (0,1] | D. | (-∞,2) |
 某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品分别可获得y1,y2万元的利润,利润曲线${P_1}:{y_1}=a{x^n}$,P2:y2=bx+c,如图所示.
某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品分别可获得y1,y2万元的利润,利润曲线${P_1}:{y_1}=a{x^n}$,P2:y2=bx+c,如图所示.