题目内容

若m＞n＞0，p＞q＞0，则一定有（　　）
A、
m
p
＞
n
q
B、
m
q
＞
n
p
C、
m
p
＜
n
q
D、
m
q
＜
n
p
考点：不等式的基本性质
专题：不等式的解法及应用
分析：由p＞q＞0，可得
1
q
＞
1
p
＞0，又m＞n＞0，可得
m
q
＞
n
p
．即可得出．
解答： 解：∵p＞q＞0，
∴
1
q
＞
1
p
＞0，
又m＞n＞0，
∴
m
q
＞
n
p
．
故选：B．
点评：本题考查了不等式的基本性质，属于基础题．
练习册系列答案
相关题目
若直线l1：2x+（m+1）y+4=0与直线l2：x+3y-2=0平行，则m的值为
 
．
一个集合的所有真子集共有n个，则n不可能取以下哪个数（　　）
A、0B、1C、2D、3
求下列函数的定义域
（1）y=
1-x
+
x+3
-1；
（2）y=
1
2-|x|
+
x2-1
．
一批种子的发芽率为80%，现播下100粒该种种子，则发芽的种子数X的均值为（　　）
A、60B、70C、80D、90
已知向量
a
=（sinx，
3
4
），
b
=（cosx，-1）．
（1）当
a
∥
b
时，求tan（x-
π
4
）的值；
（2）设函数f（x）=2（
a
+
b
）•
b
，当x∈[0，
π
2
]时，求f（x）的值域．
已知函数f（x）=[ax2+（a-1）2x+a-（a-1）2]ex（其中a∈R）．
（Ⅰ）若x=0为f（x）的极值点，求a的值；
（Ⅱ）在（Ⅰ）的条件下，解不等式f(x)＞(x-1)(
1
2
x2+x+1)．
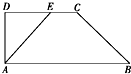如图所示，在直角梯形ABCD中，AD⊥AB且AB=7，AD=3，CD=4，DE=3，若沿AE折起，使得平面ADE⊥平面ABCE，则四棱锥D-ABCE的外接球的体积为
 
．
已知f（x）是定义在R上的偶函数，g（x）是定义在R上的奇函数，且g（x）=f（x-1），则f（2015）的值为（　　）
A、-1B、1C、0D、无法确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网