Question

【题目】已知锐角三角形的外接圆半径是，点，，分别在边，，上。求证：，，是的三条高的充要条件是，式中是的面积。

Answer 1

【答案】见解析

【解析】

△ABC的外接圆的圆心为O, ,连接, .

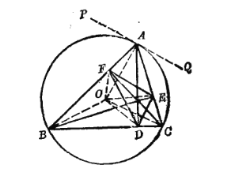
证法一:必要性因△ABC为锐角三角形,故点O在△ABC内.于是,

过点A作⊙O的切线PQ,则.

又B,C,E,F四点共圆,

∴

于是,

PQ∥E, .

.

同理,

.

从而,

充分性,设

先证.用反证法.若OA与EF不垂直,则.

又,

.

所以, .

这和已知条件矛盾.故

同理

过点A作⊙O的切线PQ,则

∵,∴PQ∥EF,,

因此,B,C,E,F四点共圆,

同理A,B,D,E四点共圆,C,A,F,D四点共圆,

故,,

于是, .

又四点共圆,

,

∴

,

即.

证法二:因为锐角三角形,故

点在内.

∴

.

因四点共圆,故:

∴.

∴,

.

即.

同理.

从而

设是的三条高,由证法一知,,

.

又设点D,E,F分别在边BC;CA,AB上,使

由证法一知,,,

∴

若点F与F不重合,不妨设,

则.

又.

从而,矛盾.于是点F与重合.

同理,点E与E重合,点D与重合.

故AD,BE,CF是△ABC的三条高