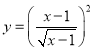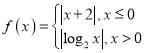Question

【题目】平面直角坐标系中，纵、横坐标都是整数的点称为整点。请设计一种方法将所有的整点染色，每一个整点染成白色、红色或黑色中的一种颜色，使得

（1）每一种颜色的点出现在无穷多条平行于横轴的直线上；

（2）对于任意白点、红点及黑点，总可以找到一个红点，使为一平行四边形。证明你设计的方法符合上述要求。

Answer 1

【答案】见解析

【解析】

我们可将整点按以下方法染色:

当是偶数时,染红色;

当为奇数时而为偶数时,染白色

当为偶数而为奇数时,染黑色.

这样染色显然符合要求(1)

以下证明这样的染色方法也符合要求,(2).

设点为白色,点为红色,点为黑色.

我们先证明不共线.事实上,与的奇偶性不同,与都是奇数,从而.

因是奇数,故;,若

则这三点不共线.

若,则

,故这三点仍不共线

因此,在任何情况下A,B,C不共线.

再取点,其中

.

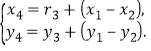显然D为整点,且因AC和BD的中点都是

所以四边形ABCD为平行四边形.

又因是偶数,故点D恰为红色点,即这样的染色方法也满足要求(2).

解二:用拉丁字母表偶数;希腊字母 表奇数.

凡纵、横坐标均为偶数的整点,即整点,…染成白色;纵、横坐标均为奇数的整点,即整点,…染成黑色;其余整点染成红色.

这样的染色方法,显然符合要求(1).

以下证明这样的染色方法也符合要求(2).

设白点A为,黑点C为,红点B为或首先,当B的坐标为时, 不共线这是因为

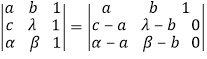
其次,线段AC的中点的坐标为,

取整点,由于为奇数, 为偶数,故D为红点,且线段的中点也是M,即相互平分,故四边形是一个平行四边形,而是这个平行四边形的四个顶点,

当B的坐标为时,同理可证结论成立.

说明:此题的第(2)条应加上“不包括蜕化的平行四边形”的条件.