题目内容
已知函数f(x)=cos2x+sinx+a,当f(x)=0时有实数解,求a的取值范围.
考点:三角函数的最值
专题:三角函数的求值
分析:令t=sinx,则由题意可得方程t2-t-1-a=0 在[-1,1]上有解.令g(t)=t2-t-1-a,再根据g(t)的最小值g(
)≤0,求得a的范围.
| 1 |
| 2 |
解答:
解:函数f(x)=cos2x+sinx+a=1-sin2x+sinx+a,
当f(x)=0时有实数解,令t=sinx,则方程-t2+t+1+a=0 在[-1,1]上有解,
即方程t2-t-1-a=0 在[-1,1]上有解.
令g(t)=t2-t-1-a,则最小值g(
)=-
-a≤0,求得a≥-
.
当f(x)=0时有实数解,令t=sinx,则方程-t2+t+1+a=0 在[-1,1]上有解,
即方程t2-t-1-a=0 在[-1,1]上有解.
令g(t)=t2-t-1-a,则最小值g(
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
点评:本题主要考查三角函数的最值,二次函数的性质应用,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
数列an=
的前5项之和是( )
| 1+(-1)n |
| 2 |
| A、0 | B、2 | C、4 | D、6 |
已知角α终边上一点的坐标是(sin
,cos
),则角α的值是( )
| π |
| 5 |
| π |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、(-1)k
|

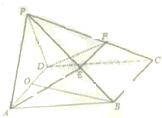 如图,已知平面PAD⊥平面ABCD,ABCD为菱形,∠BAD=60°,O是线段AD的中点,E是PB上一点,过直线AD与点E的平面与平面PBC的交线是EF.
如图,已知平面PAD⊥平面ABCD,ABCD为菱形,∠BAD=60°,O是线段AD的中点,E是PB上一点,过直线AD与点E的平面与平面PBC的交线是EF.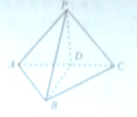 如图所示,在四面体P-ABC中,∠ABC=90°,PA=PB=PC,D是AC的中点,求证:PD垂直于△ABC所在的平面.
如图所示,在四面体P-ABC中,∠ABC=90°,PA=PB=PC,D是AC的中点,求证:PD垂直于△ABC所在的平面.