题目内容
4.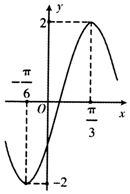 函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asinωx的图象,只需将函数y=f(x)的图象( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asinωx的图象,只需将函数y=f(x)的图象( )| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向左平移$\frac{π}{12}$个单位长度 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{12}$个单位长度 |
分析 由函数的最值求出A,由周期求出ω,由特殊点求出φ的值,可得凹函数f(x)的解析式,再利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:由函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象,
可得A=2,∵$\frac{T}{2}=\frac{π}{3}-(-\frac{π}{6})=\frac{π}{2}$,∴T=π,ω=2,f(x)=2cos(2x+φ),
将$(\frac{π}{3},2)$代入得$cos(\frac{2π}{3}+φ)=1$,∵-π<φ<0,
∴$φ=-\frac{2π}{3},f(x)=2cos(2x-\frac{2π}{3})=2sin2(x-\frac{π}{12})$.
故可将函数y=f(x)的图象向左平移$\frac{π}{12}$个单位长度得到l的图象,即可得到g(x)=Asinωx的图象,
故选:B.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由特殊点求出φ的值,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
15. 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π),其部分图象如图,则函数f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π),其部分图象如图,则函数f(x)的解析式为( )
 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π),其部分图象如图,则函数f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π),其部分图象如图,则函数f(x)的解析式为( )| A. | $f(x)=2sin({\frac{1}{2}x+\frac{π}{4}})$ | B. | $f(x)=2sin({\frac{1}{2}x+\frac{3π}{4}})$ | C. | $f(x)=2sin({\frac{1}{4}x+\frac{3π}{4}})$ | D. | $f(x)=2sin({2x+\frac{π}{4}})$ |
12.已知球的直径SC=6,A、B是该球球面上的两点,且AB=SA=SB=3,则棱锥S-ABC的体积为( )
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{{9\sqrt{2}}}{4}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{9\sqrt{2}}}{2}$ |
9.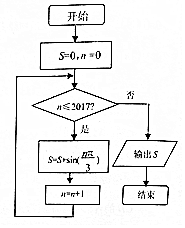 执行如图所示的程序框图,则输出S的值为( )
执行如图所示的程序框图,则输出S的值为( )
 执行如图所示的程序框图,则输出S的值为( )
执行如图所示的程序框图,则输出S的值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | 0 | D. | $\frac{1}{2}$ |
16.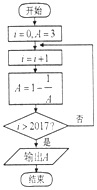 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )
 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | 3 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
13.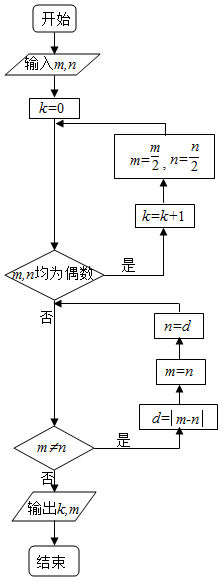 执行如图所示的程序框图,如果输入的m=168,n=112,则输出的k,m的值分别为( )
执行如图所示的程序框图,如果输入的m=168,n=112,则输出的k,m的值分别为( )
 执行如图所示的程序框图,如果输入的m=168,n=112,则输出的k,m的值分别为( )
执行如图所示的程序框图,如果输入的m=168,n=112,则输出的k,m的值分别为( )| A. | 4,7 | B. | 4,56 | C. | 3,7 | D. | 3,56 |