题目内容
9.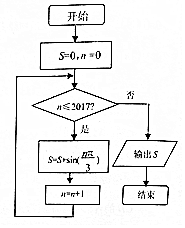 执行如图所示的程序框图,则输出S的值为( )
执行如图所示的程序框图,则输出S的值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | 0 | D. | $\frac{1}{2}$ |
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量s的值,模拟程序的运行过程,分析循环中各变量值的变化情况,利用正弦函数的周期性可得答案.
解答 解:模拟程序的运行,可得程序框图的功能是计算并输出S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+…+sin$\frac{2017π}{3}$的值,
由于sin$\frac{kπ}{3}$,k∈Z的取值周期为6,且周期内取值之和为0,2017=336×6+1,
可得:S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+…+sin$\frac{2017π}{3}$=336×0+sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$.
故选:A.
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答,属于基础题.

练习册系列答案
相关题目
17.执行如图所示的程序框图,若输入m=4,t=3,则输出y=( )


| A. | 183 | B. | 62 | C. | 61 | D. | 184 |
4.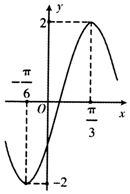 函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asinωx的图象,只需将函数y=f(x)的图象( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asinωx的图象,只需将函数y=f(x)的图象( )
 函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asinωx的图象,只需将函数y=f(x)的图象( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asinωx的图象,只需将函数y=f(x)的图象( )| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向左平移$\frac{π}{12}$个单位长度 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{12}$个单位长度 |
14.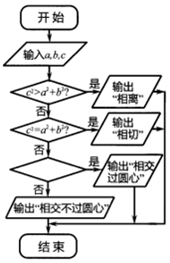 如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )
如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )
 如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )
如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )| A. | c=0? | B. | b=0? | C. | a=0? | D. | ab=0? |
12.如图,已知四边形ABCD的直观图是一个边长为1的正方形,则原图形的面积为( )


| A. | $2\sqrt{2}$ | B. | 6 | C. | 8 | D. | 4$\sqrt{2}$+2 |