题目内容
二项式(x2-
)n展开式中第三项与第五项系数之比为-
,其中i是虚数单位,则常数项为 .
| i | ||
|
| 3 |
| 14 |
考点:二项式系数的性质
专题:计算题,二项式定理
分析:利用二项展开式的通项公式求出展开式中第三项与第五项的系数,列出方程求出n;利用二项展开式的通项公式求出第r+1项,令x的指数为0求出常数项.
解答:
解:第三项的系数为-Cn2,第五项的系数为Cn4,
由第三项与第五项的系数之比为-
,可得n=10,则Tr+1=C10r(x2)10-r(-
)r=(-i)rC10rx
,
令40-5r=0,解得r=8,故所求的常数项为(-i)8C108=45,
故答案为:45.
由第三项与第五项的系数之比为-
| 3 |
| 14 |
| i | ||
|
| 40-5r |
| 2 |
令40-5r=0,解得r=8,故所求的常数项为(-i)8C108=45,
故答案为:45.
点评:本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工具.

练习册系列答案
相关题目
 如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图,设1,2两组数据的平均数依次为
如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图,设1,2两组数据的平均数依次为. |
| x1 |
. |
| x2 |
(注:标准差s=
| 1 |
| n |
(x1-
|
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知互不相同的直线l,m,n与平面α,β,则下列叙述错误的是( )
| A、若m∥l,n∥l,则m∥n |
| B、若m∥α,n∥α,则m∥n |
| C、若m⊥α,n∥β,则α⊥β |
| D、若m⊥β,α⊥β,则m∥α或m?α |
设定义在R上的函数f(x)满足f(x)•f(x+2)=13,若f(1)=2,则f(2015)=( )
| A、0 | ||
| B、2 | ||
C、
| ||
| D、13 |
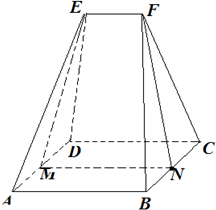 如图,五面体ABCDEF中,底面ABCD为矩形,AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6
如图,五面体ABCDEF中,底面ABCD为矩形,AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6