题目内容
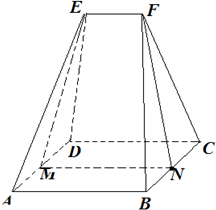如图，五面体ABCDEF中，底面ABCD为矩形，AB=6，AD=4．顶部线段EF∥平面ABCD，棱EA=ED=FB=FC=6| 2 |
| ||
| 17 |
（1）在线段BC上是否存在一点N，使BC⊥平面EFN；
（2）求平面EFB和平面CFB所成锐二面角的余弦值．
考点：二面角的平面角及求法,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（1）存在，点N为线段BC的中点，使BC⊥平面EFN．由已知得EF∥AB，MN∥AB，从而EF∥MN，E，F，M，N四点共面，由此能证明BC⊥平面EFNM．
（2）在平面EFNM内，过点F作MN的垂线，垂足为H，则二面角F-BC-A的平面角为∠FNH，过H作边AB，CD的垂线，垂足为S，Q，连接FN，FS，FQ，以H为坐标原点，以HS，HN，HF方向为x，y，z轴正方向，建立空间直角坐标系，由此能求出二面角B-EF-C的余弦值．
（2）在平面EFNM内，过点F作MN的垂线，垂足为H，则二面角F-BC-A的平面角为∠FNH，过H作边AB，CD的垂线，垂足为S，Q，连接FN，FS，FQ，以H为坐标原点，以HS，HN，HF方向为x，y，z轴正方向，建立空间直角坐标系，由此能求出二面角B-EF-C的余弦值．
解答：
解：（1）存在，点N为线段BC的中点，使BC⊥平面EFN．
证明如下：∵EF∥平面ABCD，且EF?平面EFAB，
又∵平面ABCD∩平面EFAB=AB，
∴EF∥AB（线面平行的性质定理）．
又M，N是平行四形ABCD两边AD，BC的中点，
∴MN∥AB，∴EF∥MN，∴E，F，M，N四点共面．
∵FB=FC，∴BC⊥FN，又∴BC⊥MN，
且
，∴BC⊥平面EFNM．…（6分）
（2）在平面EFNM内，过点F作MN的垂线，垂足为H，
则由（1）知：BC⊥平面EFNM，则平面ABCD⊥平面EFNM，
所以FH⊥平面ABCD，
又因为FN⊥BC，HN⊥BC，则二面角F-BC-A的平面角为∠FNH，
在Rt△FNB和Rt△FNH中，FN=
=
，
HN=FN•cos∠FNH=
•
=2．FH=8，
过H作边AB，CD的垂线，垂足为S，Q，连接FN，FS，FQ，
以H为坐标原点，以HS，HN，HF方向为x，y，z轴正方向，
建立空间直角坐标系，
则F（0，0，8），S（2，0，0），N（0，2，0），B（2，2，0），
则
=（-2，0，8），
=（0，2，0），
设平面ABEF的一个法向量为
=（x，y，z），
则
，取z=1，得
=（4，0，1），
同理可求得设平面BCF的一个法向量为
=（0，4，1），
于是有：cos＜
，
＞=
=
=
，
∴＜
1，
2＞为锐角，
设二面角B-EF-C的平面角为θ，则cosθ=cos＜
，
＞=
．…（12分）
证明如下：∵EF∥平面ABCD，且EF?平面EFAB，
又∵平面ABCD∩平面EFAB=AB，
∴EF∥AB（线面平行的性质定理）．
又M，N是平行四形ABCD两边AD，BC的中点，
∴MN∥AB，∴EF∥MN，∴E，F，M，N四点共面．
∵FB=FC，∴BC⊥FN，又∴BC⊥MN，
且
|
（2）在平面EFNM内，过点F作MN的垂线，垂足为H，
则由（1）知：BC⊥平面EFNM，则平面ABCD⊥平面EFNM，
所以FH⊥平面ABCD，
又因为FN⊥BC，HN⊥BC，则二面角F-BC-A的平面角为∠FNH，
在Rt△FNB和Rt△FNH中，FN=
| FB2-BN2 |
| 68 |
HN=FN•cos∠FNH=
| 68 |
| ||
| 17 |
过H作边AB，CD的垂线，垂足为S，Q，连接FN，FS，FQ，
以H为坐标原点，以HS，HN，HF方向为x，y，z轴正方向，
建立空间直角坐标系，
则F（0，0，8），S（2，0，0），N（0，2，0），B（2，2，0），
则
| SF |
| SB |
设平面ABEF的一个法向量为
| n1 |
则
|
| n1 |
同理可求得设平面BCF的一个法向量为
| n2 |
于是有：cos＜
| n1 |
| n2 |
| ||||
|
|
| 1 | ||||
|
| 1 |
| 17 |
∴＜
| n |
| n |
设二面角B-EF-C的平面角为θ，则cosθ=cos＜
| n1 |
| n2 |
| 1 |
| 17 |
点评：本题考查直线与平面垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
执行如图的程序框图，若输入N=2015，则输出S等于（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|