题目内容
在直三棱柱中,ABC-A′B′C′,AB=AC=AA′=2,BC=
AB且此三棱柱的各个顶点都在一个球面上,则此球的体积为 .
| 3 |
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:在△ABC中结合正余弦定理,算出它的外接圆半径R=2,设三棱柱外接球的球心为O,△ABC的外接圆心为O1,在Rt△AOO1中利用勾股定理算出OA的长,即为外接球的半径,最后根据球的体积公式,可得三棱柱外接球的体积.
解答:
解:∵△ABC中,AB=AC=2,BC=
AB=2
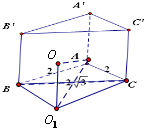
∴cos∠BAC=-
,结合∠BAC∈(0,π)得∠BAC=120°
再根据正弦定理,得△ABC的外接圆直径2R=
=4,即R=2
设三棱柱外接球的球心为O,△ABC的外接圆心为O1,则OO1=
AA'=1
可得OA=
∴外接球的体积为S=
π•OA3=
π.
故答案为:
π.
| 3 |
| 3 |

∴cos∠BAC=-
| 1 |
| 2 |
再根据正弦定理,得△ABC的外接圆直径2R=
| BC |
| sinA |
设三棱柱外接球的球心为O,△ABC的外接圆心为O1,则OO1=
| 1 |
| 2 |
可得OA=
| 5 |
∴外接球的体积为S=
| 4 |
| 3 |
20
| ||
| 3 |
故答案为:
20
| ||
| 3 |
点评:本题给出特殊三棱柱,求它的外接球体积,着重考查了直三棱柱的性质、球的体积公式和多面体的外接球等知识,属于基础题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
化简
+
(π<θ<
)( )
|
|
| 3π |
| 2 |
| A、1 | ||
| B、-1 | ||
| C、sinθ | ||
D、-
|