题目内容
8.已知正方体ABCD-A′B′C′D′的边长为a.(1)求$\overrightarrow{AC}$$•\overrightarrow{AA′}$;
(2)求$\overrightarrow{AC}$$•\overrightarrow{A′C′}$;
(3)求$\overrightarrow{AC}$•$\overrightarrow{AC′}$.
分析 以D为原点,DA为x轴,DC为y轴,DD′为z轴,建立空间直角坐标系,利用向量法能求出结果.
解答 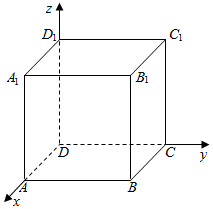 解:(1)以D为原点,DA为x轴,DC为y轴,DD′为z轴,建立空间直角坐标系,
解:(1)以D为原点,DA为x轴,DC为y轴,DD′为z轴,建立空间直角坐标系,
∵AA′⊥平面ABCD,AC?平面ABCD,
∴AC⊥AA′,
∴$\overrightarrow{AC}$$•\overrightarrow{AA′}$=0.
(2)∵AC∥A′C′,
∴$\overrightarrow{AC}$$•\overrightarrow{A′C′}$=$|\overrightarrow{AC}|$•|$\overrightarrow{{A}^{'}{C}^{'}}$|•cos0=$\sqrt{2}a•\sqrt{2}a$=2a2.
(3)$\overrightarrow{AC}$•$\overrightarrow{AC′}$=|$\overrightarrow{AC}$|•|$\overrightarrow{A{C}^{'}}$|cos∠C′AC
=$\sqrt{2}a•\sqrt{3}a$•$\frac{2{a}^{2}+3{a}^{2}-{a}^{2}}{2\sqrt{2}a•\sqrt{3}a}$=2.
点评 本题考查向量的数量积的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.在△ABC中,若${a^2}-{b^2}=\sqrt{3}bc$且$\frac{c}{b}=2\sqrt{3}$,则角A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
19.在等比数列{an}中,若有an+an-1=3•2n,则Sk+2-2Sk+1+Sk=( )
| A. | 2k | B. | 2k+1 | C. | 2k+2 | D. | 2k-1 |
3.已知:幂函数y=x3m-7(m∈N*)在区间(0,+∞)内为减函数,且幂函数的图象关于y轴对称,则m等于( )
| A. | -4 | B. | 1或2 | C. | 1 | D. | 2 |
5.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-3),若向量$\overrightarrow{c}$满足$\overrightarrow{c}$⊥$\overrightarrow{a}$,$\overrightarrow{b}$∥($\overrightarrow{a}$-$\overrightarrow{c}$),则$\overrightarrow{c}$=( )
| A. | (-$\frac{7}{4}$,$\frac{7}{8}$) | B. | ($\frac{7}{2}$,-$\frac{7}{4}$) | C. | (-$\frac{7}{2}$,-$\frac{7}{4}$) | D. | (-$\frac{7}{2}$,$\frac{7}{4}$) |