题目内容
已知{an}为等比数列，公比为q，若a2•a3=2a1，且a4与2a7的等差中项为
，则q=（ ）
| 5 |
| 4 |
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
考点：等比数列的性质,等差数列的性质
专题：计算题,等差数列与等比数列
分析：用a1和q表示出a2和a3代入a2•a3=2a1求得a4，再根据a4+2a7=a4+2a4q3，求得q．
解答：
解：∵a2•a3=a1q•a1q2=2a1
∴a4=2，
∵a4与2a7的等差中项为
，
∴a4+2a7=a4+2a4q3=2×
，
∴q=
，
故选：B．
∴a4=2，
∵a4与2a7的等差中项为
| 5 |
| 4 |
∴a4+2a7=a4+2a4q3=2×
| 5 |
| 4 |
∴q=
| 1 |
| 2 |
故选：B．
点评：本题考查了等比数列的通项公式，涉及等差数列的性质，属中档题．
练习册系列答案
相关题目
如图，运行该程序框图输出的s值为（ ）
| A、66 | B、55 | C、11 | D、10 |
执行如图所示的程序框图，若输入x=1，则输出y的值为（ ）
| A、5 | B、122 | C、14 | D、41 |
定义在R上的函数f（x）满足f（4）=1，已知f（x）的导函数f（x）′的图象如图所示，若两个正数a、b满足f（2a+b）＜1，则| a+2b+3 |
| a+1 |
A、（
| ||||
B、（-∞，
| ||||
C、（
| ||||
| D、（-∞，3） |
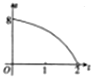
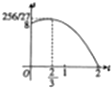
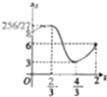
如图是一块不规则的铁皮，已知AB⊥BC，OA∥BC，AB=PC=2OA=4，曲线段OC是以点O为顶点，且开口向右的抛物线的一段，现用这块铁皮截出一块矩形铁皮，其中矩形的一对邻边分别在AB、BC上，且一个顶点P落在曲线段OC上，设点P到直线AB的距离为t+2，所截矩形铁皮的面积为S，则函数S=f（t）的图象大致是（ ）
