题目内容
20．
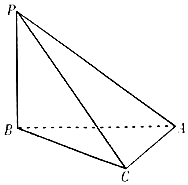如图，三棱锥P-ABC中，PB⊥BA，PC⊥CA，且PC=$\sqrt{3}CA=\sqrt{3}$，则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$．
分析 由已知得PA是三棱锥P-ABC的外接球的直径，由此能求出三棱锥P-ABC的外接球体积．
解答 解：∵三棱锥P-ABC中，PB⊥BA，PC⊥CA，且PC=$\sqrt{3}CA=\sqrt{3}$，
∴PA是三棱锥P-ABC的外接球的直径，
PA=$\sqrt{P{C}^{2}+C{A}^{2}}$=2，
∴三棱锥P-ABC的外接球体积：
V=$\frac{4}{3}π（\frac{2}{2}）^{3}$=$\frac{4π}{3}$．
故答案为：$\frac{4π}{3}$．
点评 本题考查三棱锥的外接球的体积的求法，考查推理论证能力、空间思维能力、运算求解能力，考查等价转化思想、数形结合思想，是中档题．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
11．设集合U={0，1，2，3，4}，A={0，1，3}，B={2，3，4}，则（∁UA）∩B=（ ）
| A． | {2，4} | B． | {2，3，4} | C． | {3} | D． | ∅ |
8．已知函数f（x）=x2+m与函数g（x）=-ln$\frac{1}{x}-3x（{x∈[{\frac{1}{2}，2}]}）$的图象上恰有两对关于x轴对称的点，则实数m的取值范围是（ ）
| A． | $[{\frac{5}{4}+ln2，2}）$ | B． | $[{2-ln2，\frac{5}{4}+ln2}）$ | C． | $（{\frac{5}{4}+ln2，2-ln2}]$ | D． | （2-ln2，2] |
12．
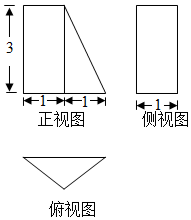已知某几何体的三视图如图所示，该几何体的体积为（ ）
已知某几何体的三视图如图所示，该几何体的体积为（ ）| A． | $\frac{2}{3}$ | B． | 2 | C． | $\frac{4}{3}$ | D． | $\frac{8}{3}$ |