题目内容
10.已知菱形ABCD的边长为2,∠ABC=60°,点E满足$\overrightarrow{BE}=\frac{1}{2}\overrightarrow{BC}$,则$\overrightarrow{AE}•\overrightarrow{AD}$=0.分析 根据菱形中的边角关系,利用平面向量的线性运算与数量积定义,计算即可.
解答 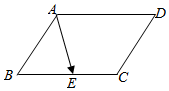 解:如图所示,
解:如图所示,
菱形ABCD的边长为2,∠ABC=60°,
$\overrightarrow{BE}=\frac{1}{2}\overrightarrow{BC}$,∴$\overrightarrow{AE}$=$\overrightarrow{AB}$+$\overrightarrow{BE}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$,
∴$\overrightarrow{AE}•\overrightarrow{AD}$=($\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$)•$\overrightarrow{AD}$
=$\overrightarrow{AB}$•$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{BC}$•$\overrightarrow{AD}$
=2×2×cos(180°-60°)+$\frac{1}{2}$×2×2
=0.
故答案为:0.
点评 本题考查了平面向量的数量积和线性运算问题,是基础题.

练习册系列答案
相关题目
18.已知θ是第四象限角,且$sin(θ+\frac{π}{4})=\frac{3}{5}$,则$tan(θ-\frac{π}{4})$=( )
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
15.已知关于x的方程sinx+cosx=m在[0,π]有两个不等的实根,则m的一个值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
2.某程序框图如图所示,该程序运行后输出的S的值是( )
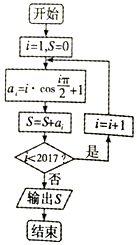

| A. | 1007 | B. | 3025 | C. | 2017 | D. | 3024 |
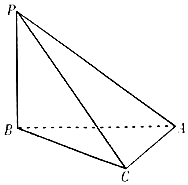 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=$\sqrt{3}CA=\sqrt{3}$,则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$.
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=$\sqrt{3}CA=\sqrt{3}$,则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$.