题目内容
15.已知函数f(x)=(x+1)ex-$\frac{1}{2}{x^2}$-ax(a∈R,e是自然对数的底数)在(0,f(0))处的切线与x轴平行.(1)求函数f(x)的单调递增区间;
(2)设g(x)=(ex+2m-2)x-$\frac{1}{2}{x^2}$-n,若?x∈R,不等式f(x)≥g(x)恒成立,求m-$\frac{n}{2}$的最大值.
分析 (1)求导,根据导数的意义得出a=2,利用导函数得出函数的单调性;
(2)不等式整理为ex≥2mx-n,恒成立问题转化为函数最值问题,构造函数h(x)=ex-2mx+n,利用导函数求出函数的最小值,进而得出结论.
解答 解:(1)f'(x)=(x+2)ex-x-a,
由已知得f'(0)=2-a=0,得a=2,
则f'(x)=(x+2)(ex-1).
令f'(x)>0,解得x>0或x<-2,
故函数的单调递增区间为(-∞,-2)和(0,+∞).
(2)不等式f(x)≥g(x),可化为ex≥2mx-n,
记h(x)=ex-2mx+n,h'(x)=ex-2m,
当m≤0时,h'(x)>0恒成立,则h(x)在R上递增,没有最小值,故不成立;
当m>0时,令h'(x)=0,解得x=ln2m,当x∈(-∞,ln2m)时,h'(x)<0;当x∈(ln2m,+∞)时,h'(x)>0,
当x=ln2m时,函数h(x)取得最小值h(ln2m)=eln2m-2mln2m+n≥0,
即2m-2mln2m≥-n,则$2m-mln2m≥m-\frac{n}{2}$,
令F(m)=2m-mln2m(m>0),F'(m)=1-ln2m,令F'(m)=0,则$m=\frac{e}{2}$,当$m∈({0,\frac{e}{2}})$时,F(m)>0;
当$m∈({\frac{e}{2},+∞})$时,F(m)<0,
故当$m=\frac{e}{2}$时,F(m)取得最大值$F({\frac{e}{2}})=\frac{e}{2}$,
所以$\frac{e}{2}≥m-\frac{n}{2}$,即$m-\frac{n}{2}$的最大值为$\frac{e}{2}$.
点评 考查了导数的意义和利用导函数求函数的单调区间,求函数的最值.难点是函数的构造和最值的求解.

| A. | y=cosx | B. | y=$\sqrt{x}$ | C. | y=2|x| | D. | y=|lgx| |
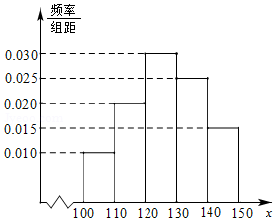 扶贫工作组帮助某村成立菠萝加工厂,加工菠萝罐头销售.在一个生产季内,销售1吨菠萝罐头可获利0.5万元,未销售的每吨亏损0.1万元.根据历年统计数据得到在生产季内菠萝罐头市场需求量x(100≤x≤150,单位:吨)的频率分布直方图如图.已知该厂在下一生产季计划生产130吨菠萝罐头.
扶贫工作组帮助某村成立菠萝加工厂,加工菠萝罐头销售.在一个生产季内,销售1吨菠萝罐头可获利0.5万元,未销售的每吨亏损0.1万元.根据历年统计数据得到在生产季内菠萝罐头市场需求量x(100≤x≤150,单位:吨)的频率分布直方图如图.已知该厂在下一生产季计划生产130吨菠萝罐头.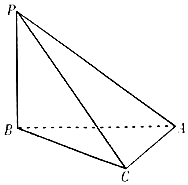 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=$\sqrt{3}CA=\sqrt{3}$,则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$.
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=$\sqrt{3}CA=\sqrt{3}$,则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$.