题目内容
5.已知椭圆C的两个焦点坐标分别是(-2,0),(2,0),并且经过$P({2,\frac{{\sqrt{6}}}{3}})$.(1)求椭圆C的标准方程;
(2)过椭圆C的右焦点F作直线l,直线l与椭圆C相交于A、B两点,当△OAB的面积最大时,求直线l的方程.
分析 (1)由题意设出椭圆方程,结合定义求得a,再由隐含条件求得b,则椭圆方程可求;
(2)设出过F(2,0)的直线的方程为:x=my+2,联立直线方程和椭圆方程,化为关于y的一元二次方程,利用弦长公式求得|AB|,再由点到直线的距离公式求得O到AB所在直线的距离,代入三角形面积公式,利用换元法求得△OAB的面积最大时的m值,则直线l的方程可求.
解答 解:(1)∵椭圆C的焦点在x轴上,∴设它的标准方程为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,
由椭圆的定义知:$2a=\sqrt{{{({2+2})}^2}+{{({\frac{{\sqrt{6}}}{3}})}^2}}+\sqrt{{{({2-2})}^2}+{{({\frac{{\sqrt{6}}}{3}})}^2}}=2\sqrt{6}$,
∴$a=\sqrt{6}$,
又∵c=2,∴b2=a2-c2=6-4=2,
因此,所求椭圆C的方程为$\frac{x^2}{6}+\frac{y^2}{2}=1$;
(2)设过F(2,0)的直线的方程为:x=my+2,
联立$\left\{{\begin{array}{l}{x=my+2}\\{\frac{x^2}{6}+\frac{y^2}{2}=1}\end{array}}\right.$,消x得:(m2+3)y2+4my-2=0,
∴${y_1}{y_2}=\frac{-2}{{{m^2}+3}},{y_1}+{y_2}=\frac{-4m}{{{m^2}+3}}$,
∴$|{AB}|=\sqrt{({1+{m^2}})[{{{({\frac{-4m}{{{m^2}+3}}})}^2}-4•\frac{-2}{{{m^2}+3}}}]}=\frac{{2\sqrt{6}({{m^2}+1})}}{{{m^2}+3}}$,
∵O到直线l的距离$d=\frac{2}{{\sqrt{{m^2}+1}}}$,
∴${S_{△OAB}}=\frac{1}{2}•\frac{{2\sqrt{6}({{m^2}+1})}}{{{m^2}+3}}•\frac{2}{{\sqrt{{m^2}+1}}}=\frac{{2\sqrt{6}\sqrt{{m^2}+1}}}{{{m^2}+3}}$,
令$t=\sqrt{{m^2}+1}$,则m2+3=t2+2,
∴${S_{△OAB}}=\frac{{2\sqrt{6}t}}{{{t^2}+2}}=\frac{{2\sqrt{6}}}{{t+\frac{2}{t}}}≤\sqrt{3}$,当且仅当$t=\frac{2}{t}$,即t2=m2+1=2,
即m=±1时,取“=”,
∴△OAB的面积最大时,直线l的方程为:x+y-2=0或x-y-2=0.
点评 本题考查椭圆的简单性质,考查直线与椭圆位置关系的应用,训练了利用换元法求函数的最值,是中档题.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年宣传费x(万元) | 38 | 48 | 58 | 68 | 78 | 88 |
| 年销售量y(吨) | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
| $\sum_{i=1}^{6}$(lnxi•lnyi) | $\sum_{i=1}^{6}$(lnxi) | $\sum_{i=1}^{6}$(lnyi) | $\sum_{i=1}^{6}$(lnxi)2 |
| 75.3 | 24.6 | 18.3 | 101.4 |
(Ⅱ)规定当产品的年销售量y(单位:吨)与年宣传费x(单位:万元)的比值在区间($\frac{e}{9}$,$\frac{e}{7}$)内时认为该年效益良好.现从这6年中任选3年,记其中选到效益良好的数量为ξ,求随机变量ξ的分布列和期望.(其中e为自然对数的底数,e≈2.7183)
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=β•u+a中的斜率和截距的最小二乘估计分别为:$\widehat{β}$=$\frac{\sum_{i=1}^{n}({u}_{i}•{v}_{i})-n(\overline{u}•\overline{v})}{{\sum_{i=1}^{n}u}_{i}^{2}-n(\overline{u})^{2}}$,$\stackrel{∧}{a}$=$\overline{v}$-$\stackrel{∧}{β}$•$\overline{u}$.
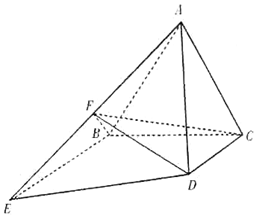 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.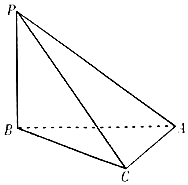 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=$\sqrt{3}CA=\sqrt{3}$,则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$.
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=$\sqrt{3}CA=\sqrt{3}$,则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$.