题目内容
已知数列{an}是等比数列，a3+a7=20，a1a9=64，求a11的值．
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：由等差数列的性质和韦达定理可得a3和a7为方程x2-20x+64=0的两根，解方程代入a11=
计算可得．
| a72 |
| a3 |
解答：
解：∵数列{an}是等比数列，a3+a7=20，a1a9=64，
∴a3a7=a1a9=64，∴a3和a7为方程x2-20x+64=0的两根，
解方程可得a3=4，a7=16或a3=16，a7=4，
当a3=4，a7=16时可得a11=
=
=64；
当a3=16，a7=4时可得a11=
=
=1
∴a3a7=a1a9=64，∴a3和a7为方程x2-20x+64=0的两根，
解方程可得a3=4，a7=16或a3=16，a7=4，
当a3=4，a7=16时可得a11=
| a72 |
| a3 |
| 162 |
| 4 |
当a3=16，a7=4时可得a11=
| a72 |
| a3 |
| 42 |
| 16 |
点评：本题考查等比数列的通项公式，涉及韦达定理和分类讨论的思想，属中档题．
练习册系列答案
相关题目
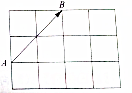如图所示是4×3的矩形（每个小方格都是单位正方形），在起点和中点都在小方格的顶点处的向量中，试问：某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、12+π | B、8+π |
| C、12-π | D、6-π |
幼儿园的一个小朋友正在给一个圆、一个三角形和一个长方形着色，有红，蓝两种颜色可供选择，对于每一个图形，他都随机地选择一种颜色涂上．
