题目内容
一个四面体的顶点在空间直角坐标系o-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以zox平面为投影面,则得到主视图可以为( )
A、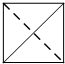 |
B、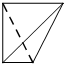 |
C、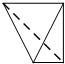 |
D、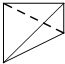 |
考点:简单空间图形的三视图
专题:作图题,空间位置关系与距离
分析:由题意画出几何体的直观图,然后判断以zOx平面为投影面,则得到正视图即可.
解答:
 解:因为一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),几何体的直观图如图,是正方体的顶点为顶点的一个正四面体,所以以zOx平面为投影面,则得到正视图为:
解:因为一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),几何体的直观图如图,是正方体的顶点为顶点的一个正四面体,所以以zOx平面为投影面,则得到正视图为:

故选A
 解:因为一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),几何体的直观图如图,是正方体的顶点为顶点的一个正四面体,所以以zOx平面为投影面,则得到正视图为:
解:因为一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),几何体的直观图如图,是正方体的顶点为顶点的一个正四面体,所以以zOx平面为投影面,则得到正视图为:
故选A
点评:本题考查几何体的三视图的判断,根据题意画出几何体的直观图是解题的关键,考查空间想象能力

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
一个几何体的三视图如图所示,如该几何体的表面积为92cm2,则h的值为( )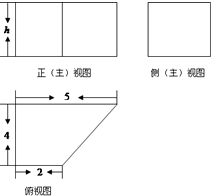

| A、4 | B、5 | C、6 | D、7 |
已知函数y=f(x)为定义在R上的奇函数,且x>0时,f(x)=lg(x2-ax+10),若函数y=f(x)的值域为R,则实数a的取值范围是( )
A、(-∞,-2
| ||||
B、(-2
| ||||
C、(-2
| ||||
D、[6,2
|