题目内容
9.设集合S={x|x2-5x+6≥0},T={x|x>1},则S∩T=( )| A. | [2,3] | B. | (1,2]∪[3,+∞) | C. | [3,+∞) | D. | (0,2]∪[3,+∞) |
分析 运用二次不等式的解法,可得S,再由交集的定义,即可得到所求.
解答 解:由集合S={x|x2-5x+6≥0}={x|x≥3或x≤2};
T={x|x>1},
所以S∩T={x|x≥3或1<x≤2},
故选:B.
点评 本题考查集合的交集运算,注意运用二次不等式的解法,以及交集的定义,考查运算能力,属于基础题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
20.“x<2”是“2x<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
14.执行如图所示的程序框图,则输出S=( )
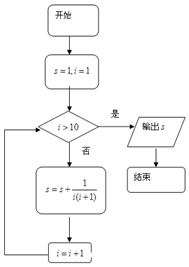

| A. | $\frac{5}{11}$ | B. | $\frac{21}{11}$ | C. | $\frac{13}{9}$ | D. | $\frac{17}{9}$ |
18.设全集U={0,1,2,3,4},集合A={0,1,3},集合B={2,3},则∁U(A∪B)=( )
| A. | {4} | B. | {0,1,2,3} | C. | {3} | D. | {0,1,2,4} |
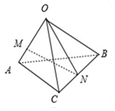 如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示) 如图,多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,平面FBC⊥平面ABCD.△FBC中BC边上的高FH=2,EF=$\frac{3}{2}$.求该多面体的体积.
如图,多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,平面FBC⊥平面ABCD.△FBC中BC边上的高FH=2,EF=$\frac{3}{2}$.求该多面体的体积.