题目内容
已知幂函数f(x)=xα的图象经过点(2,
),那么1gf(2)+1gf(5)等于( )
| 2 |
A、-
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点:幂函数的性质
专题:函数的性质及应用
分析:幂函数f(x)=xα的图象经过点(2,
),代入可得f(x)=
.再利用对数的运算性质即可得出.
| 2 |
| x |
解答:
解:∵幂函数f(x)=xα的图象经过点(2,
),
∴
=2α,解得α=
.
∴f(x)=
.
那么1gf(2)+1gf(5)=lg(
×
)=lg
=
.
故选:C.
| 2 |
∴
| 2 |
| 1 |
| 2 |
∴f(x)=
| x |
那么1gf(2)+1gf(5)=lg(
| 2 |
| 5 |
| 10 |
| 1 |
| 2 |
故选:C.
点评:本题考查了幂函数的性质、对数的运算性质,属于基础题.

练习册系列答案
相关题目
为了解2000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为( )
| A、40 | B、80 | C、50 | D、100 |
某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了解该单位职工的心理状况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,则样本容量为( )
| A、7 | B、15 | C、35 | D、25 |
i是虚数单位,记z=
,则|z|=( )
| i |
| 1+i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
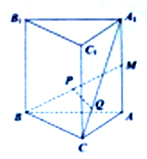 在直三棱柱ABC-A1B1C1中,若BC⊥AC,∠A=
在直三棱柱ABC-A1B1C1中,若BC⊥AC,∠A=