题目内容
设f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时f′(x)g(x)+f(x)g′(x)<0,且f(-2)=0,则不等式f(x)g(x)<0的解集是( )
| A、(-∞,-2)∪(0,2) |
| B、(-2,0)∪(0,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-2,0)∪(2,+∞) |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:设F(x)=f (x)g(x),由条件可得F(x)在(-∞,0)上为增函数,得F(x)在(0,+∞)上也为增函数.由g(-2)=0,必有F(-2)=F(2)=0,构造如图的F(x)的图象,可知F(x)<0的解集.
解答:
解:设F(x)=f (x)g(x),当x<0时,?∵F′(x)=f′(x)g(x)+f (x)g′(x)<0,
∴F(x)在(-∞,0)上为减函数.?
∵F(-x)=f (-x)g (-x)=-f (x)•g (x)=-F(x),故F(x)为(-∞,0)∪(0,+∞)上的奇函数.?
∴F(x)在(0,+∞) 上亦为减函数.
已知g(-2)=0,必有F(-2)=F(2)=0,构造如图的F(x)的图象,
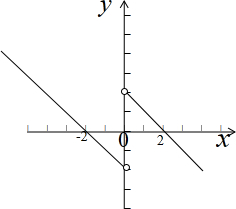
可知F(x)<0的解集为x∈(-2,0)∪(2,+∞).?
故选:D.
∴F(x)在(-∞,0)上为减函数.?
∵F(-x)=f (-x)g (-x)=-f (x)•g (x)=-F(x),故F(x)为(-∞,0)∪(0,+∞)上的奇函数.?
∴F(x)在(0,+∞) 上亦为减函数.
已知g(-2)=0,必有F(-2)=F(2)=0,构造如图的F(x)的图象,

可知F(x)<0的解集为x∈(-2,0)∪(2,+∞).?
故选:D.
点评:本题主要考查复合函数的求导运算和函数的单调性与其导函数正负之间的关系,函数的奇偶性和单调性的应用,属于基础题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知数列{an}中,an+1=an+2,则数列{an}是( )
| A、递增数列 | B、递减数列 |
| C、常数列 | D、以上都不对 |
设a,b是夹角为30°的异面直线,则满足条件“a⊆α,b⊆β,且α⊥β”的平面α,β( )
| A、不存在 | B、有且只有一对 |
| C、有且只有两对 | D、有无数对 |
抛物线y=4x2关于直线x-y=0对称的抛物线的准线方程是( )
| A、y=-1 | ||
B、y=-
| ||
| C、x=-1 | ||
D、x=-
|
已知抛物线y=
x2的焦点为F,定点M(1,2),点A为抛物线上的动点,则|AF|+|AM|的最小值为( )
| 1 |
| 4 |
A、
| ||
B、
| ||
| C、3 | ||
| D、5 |
在数列{an}中,a1=1,an+1=
(n∈N*),则a3的值为( )
| 2an |
| an+2 |
A、
| ||
B、
| ||
C、
| ||
D、
|