题目内容
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),若直线y=kx与函数y=f(x)的图象恰有3个不同的公共点,则实数k的取值范围为 .
考点:抽象函数及其应用
专题:函数的性质及应用
分析:求出函数在x∈[1,2]的函数的解析式,通过函数的奇偶性,求出函数在x∈[1,2]相切,求出切线的斜率即可求出实数k的最大值.
解答:
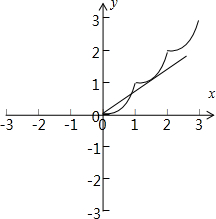 解:当0≤x≤1时,f(x)=x2,
解:当0≤x≤1时,f(x)=x2,
∴f(1)=1,
∵当x>0时,f(x+1)=f(x)+f(1),
∴当1≤x≤2时,f(x)=f(x-1)+f(1)=(x-1)2+1,
∵f(x)是定义在R上的奇函数,直线y=kx与函数y=f(x)的图象恰有3个不同的公共点,
∴x>0时,两个函数的图象,只有2个交点,如图:
设切点为(a,f(a)).
f′(x)=2x-2.
则:
=2a-2,解得a=
.
∴k=2
-2.
∴当0<k<2
-2.
此时有1个交点,x<0时,也有1个交点,x=0也是交点,
∴直线y=kx与函数y=f(x)的图象恰有3个不同的公共点,实数k的取值范围为:0<k<2
-2
故答案为:0<k<2
-2
 解:当0≤x≤1时,f(x)=x2,
解:当0≤x≤1时,f(x)=x2,∴f(1)=1,
∵当x>0时,f(x+1)=f(x)+f(1),
∴当1≤x≤2时,f(x)=f(x-1)+f(1)=(x-1)2+1,
∵f(x)是定义在R上的奇函数,直线y=kx与函数y=f(x)的图象恰有3个不同的公共点,
∴x>0时,两个函数的图象,只有2个交点,如图:
设切点为(a,f(a)).
f′(x)=2x-2.
则:
| a2-2a+2 |
| a |
| 2 |
∴k=2
| 2 |
∴当0<k<2
| 2 |
此时有1个交点,x<0时,也有1个交点,x=0也是交点,
∴直线y=kx与函数y=f(x)的图象恰有3个不同的公共点,实数k的取值范围为:0<k<2
| 2 |
故答案为:0<k<2
| 2 |
点评:本题考查抽象函数及其应用,着重考查函数的零点与方程根的关系,考查函数的对称性、周期性、奇偶性的综合应用,考查转化思想与作图能力,属于难题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
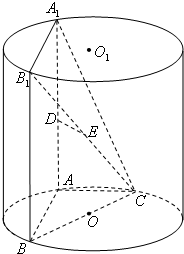 如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.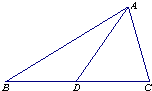 如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=
如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=