题目内容
11.下表是某地收集到的新房屋的销售价格y(单位:万元)和房屋的面积x(单位:m2)的数据:| x | 115 | 110 | 80 | 135 | 105 |
| y | 44.8 | 41.6 | 38.4 | 49.2 | 42 |
(2)求线性回归方程.
分析 (1)根据表中所给的五对数据,在平面直角坐标系中描出这五个点,得到这组数据的散点图.
(2)根据表中所给的数据,求出横标和纵标的平均数,把求得的数据代入求线性回归方程的系数的公式,利用最小二乘法得到结果,写出线性回归方程
解答 解:(1)散点图如图所示: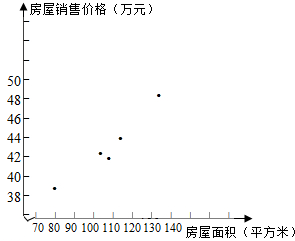
(2)计算$\overline{x}$=$\frac{1}{5}$(115+110+80+135+105)=109,
$\overline{y}$=$\frac{1}{5}$(44.8+41.6+38.4+49.2+42)=43.2,
$\sum_{i=1}^{5}$${{x}_{i}}^{2}$=1152+1102+802+1352+1052=60975,
$\sum_{i=1}^{5}$(xiyi)=115×44.8+110×41.6+80×38.4+135×49.2+105×42=23852;
设所求回归直线方程为$\stackrel{∧}{y}$=bx+a,则b=$\frac{23852-5×109×43.2}{60975-5{×109}^{2}}$≈0.1962,
∴a=$\overline{y}$-b$\overline{x}$≈21.82;
故所求回归直线方程为$\stackrel{∧}{y}$=0.1962x+21.82.
点评 本题考查线性回归方程的求法和应用,解决本题的关键是利用最小二乘法求线性回归方程的系数时,不要弄错数据

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
2.关于x的函数f(x)=cosx+sinα,则f′(0)等于( )
| A. | 0 | B. | -1 | C. | 1 | D. | ±1 |
19.3<m<5是方程$\frac{{x}^{2}}{m-5}$+$\frac{{y}^{2}}{{m}^{2}-m-6}$=1表示的图形为双曲线的( )
| A. | 充分但非必要条件 | B. | 必要但非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分又非必要条件 |
6.设集合M={x|x=$\frac{kπ+π}{2}$-$\frac{π}{4}$,k∈Z},N={x|x=$\frac{kπ}{4}$+$\frac{π}{2}$,k∈Z},则( )
| A. | M=N | B. | M?N | C. | M⊆N | D. | M?N |
2.函数$y=4sin(2x-\frac{π}{6})$的一条对称轴方程是( )
| A. | x=-$\frac{π}{12}$ | B. | x=0 | C. | x=$\frac{π}{6}$ | D. | x=$\frac{π}{3}$ |
7.若x+y=2,则2x+2y的最小值是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |