题目内容
“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时，给出的区间内的一个数，该数越接近10表示越满意，为了解某大城市市民的幸福感，随机对该城市的男、女各500人市民进行了调查，调查数据如下表所示：| 幸福感指数 | [0，2） | [2，4） | [4，6） | [6，8） | [8，10） |
| 男市民人数 | 10 | 20 | 220 | 125 | 125 |
| 女市民人数 | 10 | 10 | 180 | 175 | 125 |
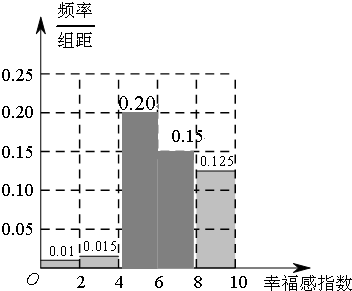
（Ⅰ）完成频率分布直方图，并根据频率分布直方图估算该城市市民幸福感指数的平均值；（参考数据：2×1+3×3+40×5+30×7+25×9=646）
（Ⅱ）如果市民幸福感指数达到6，则认为他幸福．据此，在该市随机调查5对夫妇，求他们之中恰好有3对夫妇二人都幸福的概率．（以样本的频率作为总体的概率）
考点：二项分布与n次独立重复试验的模型,频率分布直方图
专题：应用题,概率与统计
分析：（Ⅰ）由调查数据能作出频率分布直方图，并能求出该地区居民幸福感指数的平均值．
（Ⅱ）先求出男、女市民幸福的概率，可得一对夫妇都幸福的概率，从而可求他们之中恰好有3对夫妇二人都幸福的概率．
（Ⅱ）先求出男、女市民幸福的概率，可得一对夫妇都幸福的概率，从而可求他们之中恰好有3对夫妇二人都幸福的概率．
解答：
解：（Ⅰ）幸福感指数在[4，6），[6，8）内的频数分别为220+180=400和125+175=300，
因为总人数为1000，
所以，相应的频率÷组距为：400÷1000÷2=0.2，300÷1000÷2=0.15，
据此可补全频率分布直方图如右图．
所求的平均值为0.01×2×1+0.015×2×3+0.2×2×5+0.15×2×7+0.125×2×9=6.46；
（Ⅱ）男市民幸福的概率是
=0.5，
女市民幸福的概率是
=0.6，
一对夫妇都幸福的概率是0.5×0.6=0.3，
故所求的概率为
•0．33•0．72=0.1323．
解：（Ⅰ）幸福感指数在[4，6），[6，8）内的频数分别为220+180=400和125+175=300，因为总人数为1000，
所以，相应的频率÷组距为：400÷1000÷2=0.2，300÷1000÷2=0.15，
据此可补全频率分布直方图如右图．
所求的平均值为0.01×2×1+0.015×2×3+0.2×2×5+0.15×2×7+0.125×2×9=6.46；
（Ⅱ）男市民幸福的概率是
| 125+125 |
| 500 |
女市民幸福的概率是
| 175+125 |
| 500 |
一对夫妇都幸福的概率是0.5×0.6=0.3，
故所求的概率为
| C | 3 5 |
点评：本题考查频率直方图的应用，考查概率的计算，是中档题，解题时要认真审题．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
过点（1，2）且与直线3x-2y-1=0平行的直线方程是（ ）
| A、3x-2y+1=0 |
| B、2x-3y+1=0 |
| C、3x-2y+2=0 |
| D、2x-3y+2=0 |
设函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜
）的图象关于直线x=
π对称，且它的最小正周期为π，则（ ）
| π |
| 2 |
| 2 |
| 3 |
A、f（x）在区间[
| ||||
B、f（x）的图象经过点（0，
| ||||
C、f（x）的图象沿着x轴向右平移
| ||||
D、f（x）在[0，
|
已知圆C：x+（y-1）2=
直线l：y=
x将l绕原点按逆时针方向旋转θ（θ为锐角）第一次与圆C相切，则tanθ的值是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|