题目内容
已知等比数例{an}的公比q>1,a1,a2是方程x2-3x+2=0的两根,
(1)求数列{an}的通项公式;
(2)求数列{2n•an}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)求数列{2n•an}的前n项和Sn.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)依题意,易求a1=1,a2=2,从而得q=2,于是可得数列{an}的通项公式;
(2)由(1)知2n•an=n•2n,Sn=1×2+2×22+…+n×2n,利用错位相减法即可求得数列{2n•an}的前n项和Sn.
(2)由(1)知2n•an=n•2n,Sn=1×2+2×22+…+n×2n,利用错位相减法即可求得数列{2n•an}的前n项和Sn.
解答:
解:(1)方程x2-3x+2=0的两根分别为1、2,…(1分)
依题意得a1=1,a2=2,…(2分)
所以q=2,…(3分)
所以数列{an}的通项公式为an=2n-1;…(4分)
(2)由(1)知2n•an=n•2n,…(5分)
所以Sn=1×2+2×22+…+n×2n,①
2•Sn=1×22+2×23+…+(n-1)•2n+n×2n+1,②
由①-②得:
-Sn=2+22+23+…+2n-n×2n+1,…(8分)
即-Sn=
-n×2n+1,…(11分)
所以Sn=2+(n-1)•2n+1…(12分)
依题意得a1=1,a2=2,…(2分)
所以q=2,…(3分)
所以数列{an}的通项公式为an=2n-1;…(4分)
(2)由(1)知2n•an=n•2n,…(5分)
所以Sn=1×2+2×22+…+n×2n,①
2•Sn=1×22+2×23+…+(n-1)•2n+n×2n+1,②
由①-②得:
-Sn=2+22+23+…+2n-n×2n+1,…(8分)
即-Sn=
| 2-2n•2 |
| 1-2 |
所以Sn=2+(n-1)•2n+1…(12分)
点评:本题主要考查一元二次方程的根、等比数列的通项公式、错位相减法求数列的和等基本知识,考查应用能力、运算求解能力,考查函数与方程思想.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
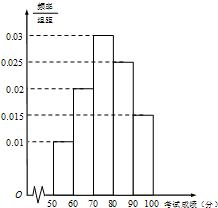 某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100]. 设k是一个正整数,(1+
设k是一个正整数,(1+