题目内容
9.在${(\sqrt{x}+\frac{1}{{2•\root{4}{x}}})^n}$的展开式中,前三项的系数成等差数列.(Ⅰ)求展开式中含有x的项的系数;
(Ⅱ)求展开式中的有理项.
分析 (I)根据前三项系数成等差数列计算n,再根据通项得出答案;
(II)根据通项判断x的次数为整数时对应的r,得出对应的项.
解答 解:(I)${(\sqrt{x}+\frac{1}{{2•\root{4}{x}}})^n}$的展开式的通项Tr+1=${C}_{n}^{r}$($\sqrt{x}$)n-r•$\frac{1}{{2}^{r}}$•($\frac{1}{\root{4}{x}}$)r=$\frac{1}{{2}^{r}}$${C}_{n}^{r}$•x${\;}^{\frac{2n-3r}{4}}$,
∴展开式的前三项系数分别为1,$\frac{n}{2}$,$\frac{n(n-1)}{8}$,
∴1+$\frac{n(n-1)}{8}$=n,解得n=1(舍)或n=8.
令$\frac{2n-3r}{4}$=1得r=4.
∴展开式中含有x的项的系数为$\frac{1}{{2}^{4}}$•${C}_{8}^{4}$=$\frac{35}{8}$.
(II)Tr+1=$\frac{1}{{2}^{r}}$${C}_{8}^{r}$x${\;}^{\frac{16-3r}{4}}$,
∴当r=0时,$\frac{16-3r}{4}$=4,T1=${C}_{8}^{0}$x4=x4.
当r=4时,$\frac{16-3r}{4}$=1,T5=$\frac{1}{{2}^{5}}$${C}_{8}^{5}$x=$\frac{14}{13}$x.
当r=8时,$\frac{16-3r}{4}$=-2,T9=$\frac{1}{{2}^{8}}$${C}_{8}^{8}$x-2=$\frac{1}{256{x}^{2}}$.
∴展开式中的有理项为x4,$\frac{14}{13}$x;$\frac{1}{256{x}^{2}}$.
点评 本题考查了二项式定理,属于中档题.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案| A. | -$\frac{8}{15}$ | B. | -$\frac{29}{15}$ | C. | -$\frac{27}{20}$ | D. | $\frac{1}{20}$ |
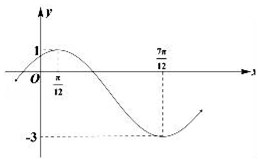 已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示:
已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示: