题目内容
19.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-3,4).(1)求$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角;
(2)若$\overrightarrow{c}$满足$\overrightarrow{c}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),($\overrightarrow{c}$+$\overrightarrow{a}$)∥$\overrightarrow{b}$,求$\overrightarrow{c}$的坐标.
分析 (1)求得$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$的坐标,利用两个向量的数量积公式、两个向量的数量积的定义,求得cosθ的值,可得$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$的夹角θ的值.
(2)根据两个向量垂直、平行的性质,求得$\overrightarrow{c}$的坐标.
解答 解:(I)∵$\overrightarrow a=(1,2),\overrightarrow b=(-3,4)$,∴$\overrightarrow a+\overrightarrow b=(-2,6)$,∴$\overrightarrow a-\overrightarrow b=(4,-2)$,
∴$(\overrightarrow a+\overrightarrow b)•(\overrightarrow a-\overrightarrow b)=-20$,∴$|{\overrightarrow a+\overrightarrow b}|=\sqrt{(-2{)^2}+{6^2}}=2\sqrt{10}$,∴$|{\overrightarrow a-\overrightarrow b}|=\sqrt{{4^2}+{{(-2)}^2}}=2\sqrt{5}$.
设$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$的夹角为θ,则$cosθ=\frac{(\overrightarrow a+\overrightarrow b)•(\overrightarrow a-\overrightarrow b)}{{|{\overrightarrow a+\overrightarrow b}|.|{\overrightarrow a-\overrightarrow b}|}}=\frac{-20}{{2\sqrt{10}×2\sqrt{5}}}=-\frac{{\sqrt{2}}}{2}$.
又∵θ∈[0,π],∴$θ=\frac{3π}{4}$.
(II)设$\overrightarrow c=(x,y)$,则$\overrightarrow c+\overrightarrow a=(x+1,y+2)$,∵$\overrightarrow{c}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),($\overrightarrow{c}$+$\overrightarrow{a}$)∥$\overrightarrow{b}$,∴$\left\{\begin{array}{l}-2x+6y=0\\-3(y+2)-4(x+1)=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=-2\\ y=-\frac{2}{3}\end{array}\right.$,即$\overrightarrow c=(-2,-\frac{2}{3})$.
点评 本题主要考查两个向量的数量积公式,两个向量坐标形式的运算法则,两个向量垂直、平行的性质,属于基础题.

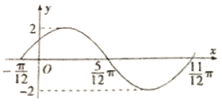 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示.