题目内容
下列说法正确的是( )
| A、“p∨q为真”是“p∧q为真”的充分不必要条件 | ||||
| B、已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | ||||
C、若a,b∈[0,1],则不等式a2+b2<
| ||||
| D、已知空间直线a,b,c,若a⊥b,b⊥c,则a∥c |
考点:命题的真假判断与应用
专题:简易逻辑
分析:必须对选项一一加以判断:对A应用充分必要条件定义考虑;对B由正态分布的知识可得;对C应用几何概率的知识可得;对D应用空间两直线的位置关系判断.
解答:
解:对A,因为“p∨q为真”不一定“p∧q为真”,所以A不对;
对B,因为随机变量X~N(2,σ2),且P(X≤4)=0.84,所以随机变量X服从正态分布N(2,σ2),
μ=2,所以p(X≤0)=p(X≥4)=1-p(X≤4)=0.16. 故B对;
对C,这是几何概型问题.其中区域D:边长为1的正方形,区域d:半径为
的第一象限内的
圆,测度为面积,
所以则不等式a2+b2<
成立的概率是
,故C错;
对D,若空间直线a,b,c满足a⊥b,b⊥c,则a,c平行或相交或异面,所以D错.
故选:B.
对B,因为随机变量X~N(2,σ2),且P(X≤4)=0.84,所以随机变量X服从正态分布N(2,σ2),
μ=2,所以p(X≤0)=p(X≥4)=1-p(X≤4)=0.16. 故B对;
对C,这是几何概型问题.其中区域D:边长为1的正方形,区域d:半径为
| 1 |
| 2 |
| 1 |
| 4 |
所以则不等式a2+b2<
| 1 |
| 4 |
| π |
| 16 |
对D,若空间直线a,b,c满足a⊥b,b⊥c,则a,c平行或相交或异面,所以D错.
故选:B.
点评:本题主要考查充分必要条件的判断以及随机变量中正态分布、概率中的几何概率、空间两直线的位置关系,解题时必须对每一个选项考虑,还应注意选正确的,还是错误的,是一道基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 一个侧棱与底面垂直的棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则截去那一部分的体积为.( )
一个侧棱与底面垂直的棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则截去那一部分的体积为.( )| A、1 | ||
B、
| ||
| C、11 | ||
| D、12 |
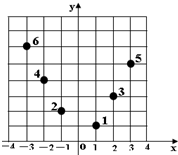 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示:
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示:| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
| A、501 | B、502 |
| C、503 | D、504 |
下列命题正确的是( )
A、
| ||||||||
| B、对任意的实数x,都有x3≥x2-x+1恒成立. | ||||||||
C、y=
| ||||||||
| D、y=2x(2-x),(x≥2)的最大值为2 |
复数z=
的虚部为( )
| 2 |
| -1+i |
| A、-1 | B、-i | C、1 | D、i |
 已知某几何体的三视图如图,其中主视图中半圆直径为2,则该几何体的体积
已知某几何体的三视图如图,其中主视图中半圆直径为2,则该几何体的体积