题目内容
α∈(0,
),cos2α+2msinα-2m-2<0恒成立,求m的取值范围.
| π |
| 2 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:已知不等式左边第一项利用同角三角函数间的基本关系化简,整理后令sinα=t,t∈[-1,1],利用二次函数的性质及根的判别式列出关于m的不等式,求出不等式的解集即可确定出m的范围.
解答:
解:已知不等式变形得:1-sin2α-2msinα-2m-2<0,
整理得:sin2α+2msinα+2m+1>0,
令sinα=t,t∈[-1,1],
得到t2+2mt+2m+1>0恒成立,即△=4m2-4(2m+1)<0,
整理得:(m-1)2<2,
解得:-
+1<m<
+1,
则m的取值范围为(-
+1,
+1).
整理得:sin2α+2msinα+2m+1>0,
令sinα=t,t∈[-1,1],
得到t2+2mt+2m+1>0恒成立,即△=4m2-4(2m+1)<0,
整理得:(m-1)2<2,
解得:-
| 2 |
| 2 |
则m的取值范围为(-
| 2 |
| 2 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列说法正确的是( )
| A、“p∨q为真”是“p∧q为真”的充分不必要条件 | ||||
| B、已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | ||||
C、若a,b∈[0,1],则不等式a2+b2<
| ||||
| D、已知空间直线a,b,c,若a⊥b,b⊥c,则a∥c |

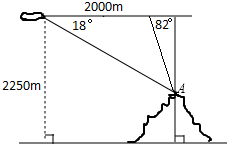 如图,一只气球在2250m的高空水平飞行,气球上的工作人员测得前方一座山顶上A点处的俯角为18°,当气球向前飞行了2000m后,又测得前方A点处的俯角为82°,则山的高度为
如图,一只气球在2250m的高空水平飞行,气球上的工作人员测得前方一座山顶上A点处的俯角为18°,当气球向前飞行了2000m后,又测得前方A点处的俯角为82°,则山的高度为