题目内容
已知集合A={x|1<ax+2≤6},集合B={x|-
<x≤3},
(1)若A⊆B,求实数a的取值范围;
(2)若B⊆A,求实数a的取值范围.
| 1 |
| 3 |
(1)若A⊆B,求实数a的取值范围;
(2)若B⊆A,求实数a的取值范围.
考点:集合的包含关系判断及应用
专题:集合
分析:根据集合的包含关系,列出不等式,求出实数a的取值范围
解答:
解:∵集合A={x|1<ax+2≤6},
∴①a=0时,A=R
②a>0,A=(-
,
】
③a<0,A=[
,-
)
(1)∵集合B={x|-
<x≤3},若A⊆B,
∴a=0时不满足
或
,即a≥3
或
,即a<-12
综上所述,A⊆B,求实数a的取值范围:a≥3或a<-12
(2)若B⊆A
,a<3
或
,即a≥-12
综上所述,B⊆A,求实数a的取值范围:-12≤a<3
∴①a=0时,A=R
②a>0,A=(-
| 1 |
| a |
| 4 |
| a |
③a<0,A=[
| 4 |
| a |
| 1 |
| a |
(1)∵集合B={x|-
| 1 |
| 3 |
∴a=0时不满足
或
|
或
|
综上所述,A⊆B,求实数a的取值范围:a≥3或a<-12
(2)若B⊆A
|
或
|
综上所述,B⊆A,求实数a的取值范围:-12≤a<3
点评:本题主要考查集合的基本运算,属于基础题.要正确判断两个集合间的关系,必须对集合的相关概念有深刻的理解,善于抓住代表元素,认清集合的特征.

练习册系列答案
相关题目
下列说法正确的是( )
| A、“p∨q为真”是“p∧q为真”的充分不必要条件 | ||||
| B、已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | ||||
C、若a,b∈[0,1],则不等式a2+b2<
| ||||
| D、已知空间直线a,b,c,若a⊥b,b⊥c,则a∥c |
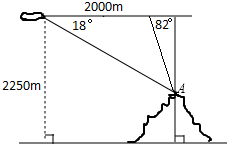 如图,一只气球在2250m的高空水平飞行,气球上的工作人员测得前方一座山顶上A点处的俯角为18°,当气球向前飞行了2000m后,又测得前方A点处的俯角为82°,则山的高度为
如图,一只气球在2250m的高空水平飞行,气球上的工作人员测得前方一座山顶上A点处的俯角为18°,当气球向前飞行了2000m后,又测得前方A点处的俯角为82°,则山的高度为