题目内容
已知函数f(x)=log
(1)求f(x)的定义域;
(2)讨论函数f(x)的单调性;
(3)解不等式f(x)>0.
(
|
(1)求f(x)的定义域;
(2)讨论函数f(x)的单调性;
(3)解不等式f(x)>0.
考点:指、对数不等式的解法,函数的定义域及其求法,复合函数的单调性
专题:函数的性质及应用
分析:(1)只要解不等式
-1>0即可;
(2)利用复合函数的单调性的判断将f(x)分解为两个简单函数,然后利用同增异减的原则判断;
(3)利用对数函数的单调性得到真数的大小.
| 1 |
| 2x |
(2)利用复合函数的单调性的判断将f(x)分解为两个简单函数,然后利用同增异减的原则判断;
(3)利用对数函数的单调性得到真数的大小.
解答:
解:(1)f(x)的定义域是使
-1>0的x的范围,解得x<0,所以函数的定义域为{x|x<0};
(2)因为t=
-1是减函数,y=log
t也是减函数,所以f(x)=log
在定义域内是增函数;
(3)不等式f(x)>0即log
>0,所以0<
-1<1,解得0<x<1.
| 1 |
| 2x |
(2)因为t=
| 1 |
| 2x |
| 1 |
| 2 |
(
|
(3)不等式f(x)>0即log
(
|
| 1 |
| 2x |
点评:本题考查了对数型函数的定义域、单调性和对数不等式的解法;复合函数的单调性遵循同增异减的原则.

练习册系列答案
相关题目
复数z在复平面内的对应点为(-1,1),
是z的共轭复数,则
+|z|=( )
. |
| z |
| 2 |
. |
| z |
A、
| ||
B、-
| ||
C、
| ||
D、
|
下列判断错误的是( )
| A、“am2<bm2”是“a<b”的充分不必要条件 |
| B、若f′(x0)=0,则x=x0是函数y=f(x)的极值点 |
| C、函数y=f(x)满足f(x+1)=f(1-x),则其图象关于直线x=1对称 |
| D、定义在R上的函数y=f(x)满足f(x+1)=-f(x),则周期为2 |
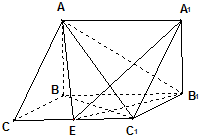 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已BC=1,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已BC=1,∠BCC1=