题目内容
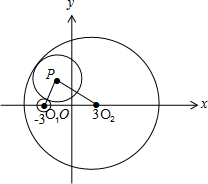
动圆P与圆O1:x2+y2+6x+8=0外切,与圆O2:x2+y2-6x-72=0内切,求动圆圆心P的轨迹.
考点:轨迹方程
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:化圆的一般方程为标准方程,求出圆心坐标和半径,数形结合可知动圆圆心P满足到两个定圆的圆心的距离和等于定长,且定长大于两圆心的距离,故动圆圆心P的轨迹是以O1,O2为焦点,长轴长为10的椭圆,则答案可求.
解答:
解:化圆O1:x2+y2+6x+8=0为(x+3)2+y2=1,
化圆O2:x2+y2-6x-72=0为(x-3)2+y2=81,
设动圆圆心P(x,y),
∵动圆P与圆O1:x2+y2+6x+8=0外切,与圆O2:x2+y2-6x-72=0内切,
∴|PO1|+|PO2|=9+1=10,
∴动圆圆心P的轨迹是以O1,O2为焦点,长轴长为10的椭圆.
则2a=10,a=5,c=3,b2=a2-c2=16.
∴动圆圆心P的轨迹为:
+
=1.
化圆O2:x2+y2-6x-72=0为(x-3)2+y2=81,
设动圆圆心P(x,y),
∵动圆P与圆O1:x2+y2+6x+8=0外切,与圆O2:x2+y2-6x-72=0内切,
∴|PO1|+|PO2|=9+1=10,
∴动圆圆心P的轨迹是以O1,O2为焦点,长轴长为10的椭圆.
则2a=10,a=5,c=3,b2=a2-c2=16.
∴动圆圆心P的轨迹为:
| x2 |
| 25 |
| y2 |
| 16 |

点评:本题考查了轨迹方程,考查了椭圆的定义,训练了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
已知△ABC中,BC=3,AC=4,AB=5点P是三边上的任意一点,m=
•
,则m的最小值是( )
| PA |
| PB |
| A、-25 | ||
B、-
| ||
C、-
| ||
| D、0 |
原点到直线3x+2y-13=0的距离是( )
A、
| ||
| B、4 | ||
| C、1 | ||
D、
|
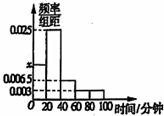 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为:[0,20),[20,40),[40,60)[60,820),[80,100],则
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为:[0,20),[20,40),[40,60)[60,820),[80,100],则 如图,正方形OABC的边长为2.在其四边或内部取点P(x,y),且x,y∈Z,则事件“|OP|>1”的概率是
如图,正方形OABC的边长为2.在其四边或内部取点P(x,y),且x,y∈Z,则事件“|OP|>1”的概率是