题目内容
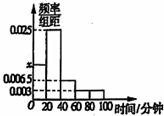 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为:[0,20),[20,40),[40,60)[60,820),[80,100],则
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为:[0,20),[20,40),[40,60)[60,820),[80,100],则(1)图中的x=
(2)若上学所需时间不少于1小时的学生可申请在学校住宿,则该校600名新生中估计
考点:频率分布直方图
专题:计算题,概率与统计
分析:(1)利用面积之和为1解出x即可;
(2)先求出上学时间不少于1小时的学生的频率,再由频率估计概率,从而求人数.
(2)先求出上学时间不少于1小时的学生的频率,再由频率估计概率,从而求人数.
解答:
解:(1)由频率分布直方图知,
20x=1-20×(0.025+0.0065+0.003+0.003),
解得x=0.0125.
(2)上学时间不少于1小时的学生频率为(0.003+0.003)×20=0.12,
因此估计有0.12×600=72名学生可以申请住宿.
故答案为:(1)0.0125;(2)72.
20x=1-20×(0.025+0.0065+0.003+0.003),
解得x=0.0125.
(2)上学时间不少于1小时的学生频率为(0.003+0.003)×20=0.12,
因此估计有0.12×600=72名学生可以申请住宿.
故答案为:(1)0.0125;(2)72.
点评:本题考查了频率分布直方图的应用及频率与概率的联系,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知f(x)的定义域为[-2,3],则f(x-1)的定义域是( )
| A、[-1,4] |
| B、[-3,2] |
| C、[-5,5] |
| D、[-3,7] |
 如图所示,液体从一圆锥形漏斗漏入圆柱形桶中,H是圆锥形漏斗中液面下降的距离,则H与下降时间t(分钟)的函数关系用图象表示只可能是( )
如图所示,液体从一圆锥形漏斗漏入圆柱形桶中,H是圆锥形漏斗中液面下降的距离,则H与下降时间t(分钟)的函数关系用图象表示只可能是( )


