题目内容
在等腰△ABC中,|AB|=|AC|,顶点A为直线l:x-y+1=0与y轴交点且l平分∠A,若B(1,3),求:
(I)直线BC的方程;
(Ⅱ)计算△ABC的面积.
(I)直线BC的方程;
(Ⅱ)计算△ABC的面积.
考点:两直线的夹角与到角问题,直线的一般式方程
专题:直线与圆
分析:(1)由条件知B和C关于直线l对称,设C(a,b),则由
求得C的坐标,可得BC方程.
(2)由于A(0,1),求得cosA=
的值,可得sinA的值,再根据S△ABC=
|
|•|
|sinA,计算求得结果.
|
(2)由于A(0,1),求得cosA=
| ||||
|
|
| 1 |
| 2 |
| AB |
| AC |
解答:
解:(1)由条件知B和C关于直线l对称,设C(a,b),则
,
可得C(2,2),所以BC方程为y-2=
(x-2),
化简得直线BC的方程为x+y-4=0.
(2)由于A(0,1),可得
=(1,3)-(0,1)=(1,2);
=(2,2)-(0,1)=(2,1),
cosA=
=
=
,
∴sinA=
,S△ABC=
|
|•|
|sinA=
,
|
可得C(2,2),所以BC方程为y-2=
| 3-2 |
| 1-2 |
化简得直线BC的方程为x+y-4=0.
(2)由于A(0,1),可得
| AB |
| AC |
cosA=
| ||||
|
|
| 2+2 | ||||
|
| 4 |
| 5 |
∴sinA=
| 3 |
| 5 |
| 1 |
| 2 |
| AB |
| AC |
| 3 |
| 2 |
点评:本题主要考查求一个点关于某直线的对称点的坐标的方法,用点斜式求直线的方程,用两个向量的数量积表示两个向量的夹角,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等差数列{an}的前n项和为Sn,an=-2n+16,则欲Sn最大,必n=( )
| A、9 | B、7 | C、8 | D、7,8 |
下列说法错误的是( )
| A、一辆汽车在高速公路上行驶的过程中,行驶路程是时间的函数 |
| B、汽车加油站常用圆柱体储油罐储存汽油,储油量是油面宽度的函数 |
| C、某十字路口,通过汽车的数量是时间的函数 |
| D、在一定量的水中加入蔗糖(非饱和溶液),所加蔗糖的质量是糖水的质量浓度的函数 |
若a≠0,b≠,则代数式
+
+
的取值共有( )
| a |
| |a| |
| b |
| |b| |
| ab |
| |ab| |
| A、2个 | B、3个 | C、4个 | D、5个 |
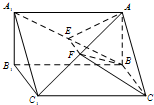 如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点.