Question

已知△ABC中，BC=3，AC=4，AB=5点P是三边上的任意一点，m=

PA

•

PB

，则m的最小值是（　　）

• A、-25
• B、-

  25

  4

• C、-

  9

  4

• D、0

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：如图所示，A（0，4），B（3，0）．分类讨论：①当点P∈BC线段时，设P（x，0），0≤x≤3．②当点P∈AC线段时，设P（0，y），0≤y≤4．③当点P∈BA线段时，设P（x，y），0≤x≤3，0≤y≤4．即可得出．

解答： 解：如图所示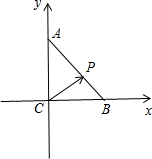，A（0，4），B（3，0）．
①当点P∈BC线段时，设P（x，0），0≤x≤3．
则m=

PA

•

PB

=（-x，4）•（3-x，0）=-x（3-x）=x²-3x=(x-

3

2

)2-

9

4

≥-

9

4

，
当且仅当x=

3

2

时取等号．
②当点P∈AC线段时，设P（0，y），0≤y≤4．
则m=

PA

•

PB

=（0，4-y）•（3，-y）=-y（4-y）=y²-4y=（y-2）²-4≥-4，
当且仅当y=2时取等号．
③当点P∈BA线段时，设P（x，y），0≤x≤3，0≤y≤4．
则m=

PA

•

PB

=（-x，4-y）•（3-x，-y）=-x（3-x）-y（4-y）=(x-

3

2

)2+(y-2)2-

25

4

，
当且仅当x=

3

2

，y=2时取等号．
综上可得：m=

PA

•

PB

的最小值为-

25

4

，此时点P为线段AB的中点．

点评：本题考查了通过建立直角坐标系利用向量的坐标运算求数量积的取值范围，考查了计算能力，属于中档题．