题目内容
已知
、
是平面内两个相互垂直的单位向量,且(3
-
)•(4
-
)=0,则|
|的最大值为 .
| α |
| β |
| α |
| γ |
| β |
| γ |
| γ |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由题意可得|
|=|
|=1,
•
=0,再根据(3
-
)•(4
-
)=0,求得|
2|≤|3
+4
|•|
|,即|
|≤|3
+4
|=
=5,从而求得|
|的最大值.
| α |
| β |
| α |
| β |
| α |
| γ |
| β |
| γ |
| γ |
| α |
| β |
| γ |
| γ |
| α |
| β |
(3
|
| γ |
解答:
解:由题意可得|
|=|
|=1,
•
=0,
∵(3
-
)•(4
-
)=0,∴
2=(3
+4
)•
,∴|
2|≤|3
+4
|•|
|,
∴|
|≤|3
+4
|=
=5,
故答案为:5.
| α |
| β |
| α |
| β |
∵(3
| α |
| γ |
| β |
| γ |
| γ |
| α |
| β |
| γ |
| γ |
| α |
| β |
| γ |
∴|
| γ |
| α |
| β |
(3
|
故答案为:5.
点评:本题主要考查两个向量的数量积公式的应用,求向量的模的方法,属于基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
函数y=3x-8+log2x的零点一定位于的区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
若{2,3}?M?{1,2,3,4,5},则M的个数为( )
| A、5 | B、6 | C、7 | D、8 |
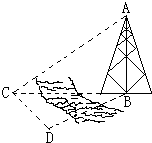 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40(米),并在点C测得塔顶A的仰角为30°.则塔高AB=
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40(米),并在点C测得塔顶A的仰角为30°.则塔高AB=