题目内容
已知f（x）为R上奇函数．当x＞0时，f（x）=x（1-x），求f（x）的表达式，并在所给坐标系中画出f（x）图象．考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数是奇函数，有f（0）=0，设x＜0，则-x＞0，代入f（x）=x（1-x），再由f（-x）=-f（x）解答即可．
解答：
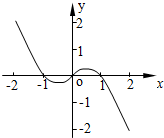解：∵f（x）为R上奇函数
∴当x=0时，f（0）=f（-0）=-f（0），∴f（0）=0
当x＜0时，则-x＞0，∴f（-x）=（-x）（1-（-x））=-x（1+x）
∵f（x）为R上奇函数，∴f（-x）=-f （x）
∴-f （x）=-x（1+x），即f （x）=x（1+x） （x＜0）
∴f(x)=
．
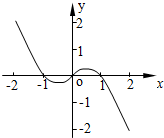解：∵f（x）为R上奇函数∴当x=0时，f（0）=f（-0）=-f（0），∴f（0）=0
当x＜0时，则-x＞0，∴f（-x）=（-x）（1-（-x））=-x（1+x）
∵f（x）为R上奇函数，∴f（-x）=-f （x）
∴-f （x）=-x（1+x），即f （x）=x（1+x） （x＜0）
∴f(x)=
|
点评：本题主要考查函数的奇偶性，注意奇函数的f（0）=0．
练习册系列答案
相关题目
已知两集合M={x∈R|0≤x≤8}，N={y∈R|0≤y≤5}．下列的对应关系中，是M到N的映射的是（ ）
A、f：x→y=2
| |||
B、f：x→y=
| |||
| C、f：x→y=2x-1 | |||
D、f：x→y=
|