题目内容
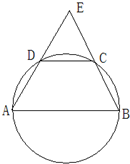 如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.(Ⅰ)证明:CB=DA;
(Ⅱ)若∠AEB=60°且D是AE的中点,证明:AB是该圆的直径.
考点:与圆有关的比例线段
专题:立体几何
分析:(I)由已知得∠EDC=∠ECD,∠EDC=∠EBA.从而∠ECD=∠EBA,同理∠EDC=∠EAB,由此能证明CB=DA.
(II)取AB的中点O,连OD,则OD=
BE.由(I)知△EDC和△EAB都是正三角形,由此能证明AB是该圆的直径.
(II)取AB的中点O,连OD,则OD=
| 1 |
| 2 |
解答:
解:(I)因为EC=ED,所以∠EDC=∠ECD.
因为A,B,C,D四点在同一圆上,
所以∠EDC=∠EBA.
故∠ECD=∠EBA,同理∠EDC=∠EAB
所以∠EAB=∠EBA,所以EA=EB,
所以CB=DA.…(5分)
(II)取AB的中点O,连OD,则OD=
BE.
由(I)知△EDC和△EAB都是正三角形,
所以OA=OB=OD
所以AB是该圆的直径. …(10分)
因为A,B,C,D四点在同一圆上,
所以∠EDC=∠EBA.

故∠ECD=∠EBA,同理∠EDC=∠EAB
所以∠EAB=∠EBA,所以EA=EB,
所以CB=DA.…(5分)
(II)取AB的中点O,连OD,则OD=
| 1 |
| 2 |
由(I)知△EDC和△EAB都是正三角形,
所以OA=OB=OD
所以AB是该圆的直径. …(10分)
点评:本题考查两线段长相等的证明,考查线段是圆的直径的证明,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
